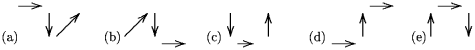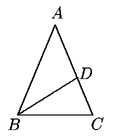Problema 76. Si el paralelogramo ABCD tiene área
1 m2 y los puntos M y N son los puntos medios
de los lados AB y CD respectivamente, ¿Qué
área tiene la región sombreada?
| (a) 3/12 |
(b) 1/3 |
(c) 5/12 |
(d) 1/2 |
(e) 7/12 |
Ver la solución
Problema 77. Dos ciclistas recorren una pista cuadrada en direcciones
opuestas. Partiendo de una esquina al mismo tiempo, la primera vez que
se encuentran es en otra esquina y la segunda en una esquina distinta de
las anteriores. Si ambos van a velocidad constante la razón de las
velocidades es:
| (a) 1:2 |
(b) 1:3 |
(c) 1:4 |
(d) 2:3 |
(e) 3:4 |
Ver la solución
Problema 78. Luis Miguel compró una bolsa con 2000 caramelos
de 5 colores; 387 de eran blancos, 396 amarillos, 402 rojos, 407 verdes
y 408 cafés. Decidió comerse los caramelos de la siguiente
forma: Sin mirar sacaba tres de la bolsa. Si los tres eran del mismo color,
se los comía, si no, los regresaba a la bolsa. Continuó así
hasta que sólo quedaron dos caramelos en la bolsa. ¿De qué
color eran?
| (a) Blancos |
(b) Amarillos |
(c) Rojos |
(d) Verdes |
(e) Cafés |
Ver la solución
Problema 79. En un triángulo ABC, siete segmentos
paralelos al lado BC y con extremos en los otros dos lados del triángulo
dividen en 8 partes iguales al lado AC. Si BC = 10, ¿cuál
es la suma de las longitudes de los siete segmentos? (Este problema
forma parte delExamen Canguro
Animado)
| (a) Faltan datos |
(b) 50 |
(c) 70 |
(d) 35 |
(e) 45 |
Ver la solución
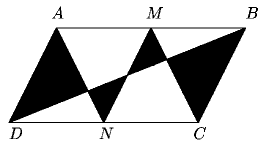
Problema 80. Un cuadrado de lado 2 se "redondea'' añadiéndole
un marco de 2 cm de ancho (en las esquinas se han puesto cuartos de círculo).
Una rueda de radio 1 cm se desplaza a lo largo del cuadrado redondeado
(siempre tocándolo). ¿Cuántas vueltas completas dará
la rueda alrededor de sí misma antes de completar una vuelta alrededor
del cuadrado redondeado? se "redondea'' añadiéndole
un marco de 2 cm de ancho (en las esquinas se han puesto cuartos de círculo).
Una rueda de radio 1 cm se desplaza a lo largo del cuadrado redondeado
(siempre tocándolo). ¿Cuántas vueltas completas dará
la rueda alrededor de sí misma antes de completar una vuelta alrededor
del cuadrado redondeado?
| (a) 3 |
(b) 6 |
(c) 8 |
(d) 10 |
(e) 12 |
Ver la solución
Problema 81. Una pedazo rectangular de piel mágica se
reduce a la mitad de su longitud y a la tercera parte de su ancho después
de cumplirle un deseo a su dueño. Después de tres deseos
tiene un área de 4 cm2. Si su ancho inicial era de 9
cm, ¿cuál era su largo inicial?
| (a) Faltan datos |
(b) 96 cm |
(c) 288 cm |
(d) 32 cm |
(e) 144 cm |
Ver la solución
Problema 82. En un campamento de verano 96 niños van
a separarse en grupos de forma que cada grupo tenga el mismo número
de niños. ¿De cuántas maneras puede hacerse la separación
si cada grupo debe de tener más de 5 pero menos de 20 niños?
| (a) 10 |
(b) 8 |
(c) 5 |
(d) 4 |
(e) 2 |
Ver la solución
Problema 83. Si haces la división de 1 entre 52000,
¿cuál será el último dígito que aparezca
antes de llegar a puros 0's?
| (a) 2 |
(b) 4 |
(c) 6 |
(d) 8 |
(e) 5 |
Ver la solución
Problema 84. ¿Cuál de los siguientes números
es más grande?
| (a) 212 |
(b) 415 |
(c) 811 |
(d) 128 |
(e) 326 |
Ver la solución
Problema 85. ¿Cuántas cifras tiene el número
21998 x 52002? (Este problema
forma parte delExamen Canguro
Animado)
| (a) 1999 |
(b) 2000 |
(c) 2001 |
(d) 2002 |
(e) 2003 |
Ver la solución
Problema 86. Omar le da a cada uno de sus libros una clave de
tres letras utilizando el orden alfabético: AAA, AAB,
AAC,...
AAZ,
ABA,
ABB,
etc. Considerando el alfabeto de 26 letras y que Omar tiene 2203 libros,
¿cuál fue el último código que Omar utilizó
en su colección?
| (a) CFS |
(b) CHT |
(c) DGS |
(d) DFT |
(e) DGU |
Ver la solución
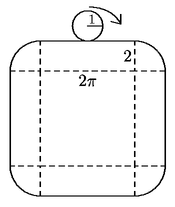
Problema 87. Se escriben los números enteros del 0 al
2000 y se dibujan flechas entre ellos con el siguiente patrón:
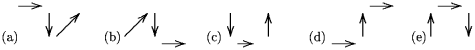 y así sucesivamente. ¿Cuál es la sucesión de
flechas que llevan del 1997 al 2000?
y así sucesivamente. ¿Cuál es la sucesión de
flechas que llevan del 1997 al 2000?

Ver la solución
Problema 88. Un pastel tiene forma de cuadrilátero. Lo
partimos por sus diagonales en cuatro partes, como se indica en la figura.
Yo me comí una parte, y después pesé las otras tres:
un pedazo de 120 g, uno de 200 g y otro de 300 g. ¿Cuánto
pesaba la parte que yo me comí?
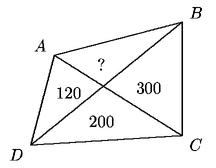
| (a) 120 |
(b) 180 |
(c) 280 |
(d) 330 |
(e) 550 |
Ver la solución
Problema 89. Tomando tres vértices cualesquiera de un
cubo se forma un triángulo. Del total de triángulos que pueden
formarse de esa manera, ¿cuántos son equiláteros?
| (a) 4 |
(b) 8 |
(c) 16 |
(d) 48 |
(e) 56 |
Ver la solución
Problema 90. En la figura, a,b,c,d,e
y f son las áreas de las regiones correspondientes. Si todos
ellos son números enteros positivos diferentes entre sí y
menores que 10, cada triángulo formado por tres regiones tiene área
par y el área de la estrella completa es 31, el valor de f
es:
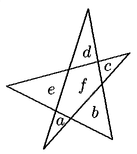
| (a) 3 |
(b) 4 |
(c) 5 |
(d) 6 |
(e) 7 |
Ver la solución
Problema 91. El círculo  de la figura tiene centro
O
y su diámetro mide 3. Los segmentos AT y RS son diámetros
perpendiculares del círculo. La recta de la figura tiene centro
O
y su diámetro mide 3. Los segmentos AT y RS son diámetros
perpendiculares del círculo. La recta  es tangente al círculo
en el punto T; B es la intersección de la recta es tangente al círculo
en el punto T; B es la intersección de la recta  con la recta AR. Calcular el área de la región
sombreada (delimitada por los segmentos BR y BT y el arco
de círculo de RT.) con la recta AR. Calcular el área de la región
sombreada (delimitada por los segmentos BR y BT y el arco
de círculo de RT.)

(a)3 /2 - 9/16 /2 - 9/16 |
(b)2 /3 /3 |
(c)9- /16 /16 |
(d)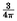
|
(e)27/8 - 9/16 |
Ver la solución
Problema 92. En la siguiente figura ABC es un triángulo
con AB=AC y D un punto sobre CA con BC=BD=DA.
El valor del ángulo ABD es:
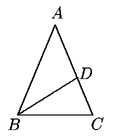
| (a) 30o |
(b) 36o |
(c) 40o |
(d) 45o |
(e) 60o |
Ver la solución
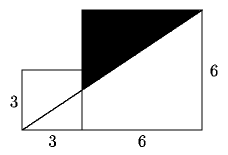
Problema 93. En la figura, cada lado del cuadrado más
pequeño mide 3 y cada lado del cuadrado más grande mide 6,
¿cuál es el área del triángulo sombreado?
| (a) 6 |
(b) 10 |
(c) 12 |
(d) 18 |
(e) 24 |
Ver la solución
Problema 94. Edgar y Raúl apostaron según las
siguientes reglas: Van a lanzar un dado normal (con los números
del 1 al 6 en sus caras) y una moneda (con los números 1 y 2 marcados
en sus caras). Después multiplicarán el número que
salga en el dado con el que salga en la moneda. Si el resultado es par
gana Edgar, y si es impar gana Raúl. ¿Qué probabilidad
de ganar tiene Edgar?
| (a) 1/2 |
(b) 1/3 |
(c) 2/3 |
(d) 3/4 |
(e) 5/6 |
Ver la solución
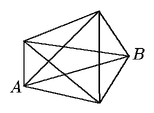
Problema 95. ¿Cuántas formas hay de llegar de
A a B si no se puede pasar dos veces por el mismo punto?
| (a) 10 |
(b) 12 |
(c) 16 |
(d) 18 |
(e) 20 |
Ver la solución
Problema 96. Si x2+y2=6xy, con
x  y, ¿a qué es igual (x+y)/(x-y)? y, ¿a qué es igual (x+y)/(x-y)?
Ver la solución
Problema 97. En un cuadrado ABCD de lado 1 está
inscrito un triángulo AEF de tal forma que E está
sobre
BC y F está sobre CD. Las longitudes
de los lados AE y AF son iguales y son el doble de la longitud
del lado EF. Calcular la longitud de EF.
(a)(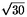 - 2)/7 - 2)/7 |
(b)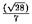 |
(c)(- + +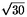 )/7 )/7 |
(d)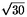 /2 /2 |
(e) - -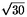 |
Ver la solución
Problema 98. En la figura, AB es el arco de un círculo
centrado en C, BC es el arco de un círculo centrado en A,
AC
es el arco de un círculo centrado en B. Si la recta
AB
mide 1, ¿Cuál es el área de la figura?
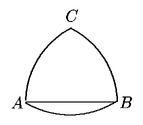 (Este problema
forma parte delExamen Canguro
Animado)
(Este problema
forma parte delExamen Canguro
Animado)
(a)2 +5/ +5/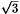 |
(b)3 - -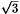 /2 /2 |
(c) ( (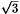 +5) +5) |
(d)( - -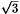 )/2 )/2 |
(e)( -5 -5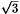 /2) /2) |
Ver la solución
Problema 99. ¿Cuál es el área del triángulo
ABC,
si AD=BD=DE,EF=2AD,CF=3AD
y el área de ADE=1?

| (a) 4.5 |
(b) 6 |
(c) 8 |
(d) 9 |
(e) 12 |
Ver la solución
Problema 100. Encontrar el valor de xyz donde x,y,z
son números positivos que satisfacen el siguiente sistema de ecuaciones:
x2 + 1/y + z = 9
x2 + 1/y - z = 3
x2 - 1/y + z = 5
| (a) 1/15 |
(b) 1/3 |
(c) 1/2 |
(d) 3 |
(e) 4 |
Ver la solución
Inicio de la página
|