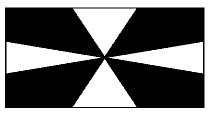
Problema 26. Cada lado de un rectángulo se divide en
tres segmentos de la misma longitud; los puntos obtenidos se unen definiendo
un punto en el centro, como se indica en la figura. ¿Cuánto
es el cociente del área de la parte blanca entre el área
de la parte gris?
| (a) 1 |
(b) 1/2 |
(c) 1/3 |
(d) 1/4 |
(e) 2/3 |
Ver la solución
Problema 27. Al aumentar en la misma proporción la longitud
de los lados de un cuadrado, su área aumenta en un 69 %. ¿Qué
porcentaje aumentaron sus lados?
| (a) 20% |
(b) 30% |
(c) 34.5% |
(d) 8.3% |
(e) 69% |
Ver la solución
Problema 28. ¿Cuánto es la suma de las cifras
del número
N=1092 - 92?
| (a) 1992 |
(b) 992 |
(c) 818 |
(d) 808 |
(e) 798 |
Ver la solución
Problema 29. Si escribí todos los números enteros
del 1 al 1000, ¿cuántas veces apareció la cifra 5?
| (a) 110 |
(b) 1331 |
(c) 555 |
(d) 100 |
(e) 300 |
Ver la solución
Problema 30. A Julio le dieron el número secreto de su
nueva tarjeta de crédito, y observó que la suma de los cuatro
dígitos del número es 9 y ninguno de ellos es 0; además
el número es múltiplo de 5 y mayor que 1995. ¿Cuál
es la tercer cifra de su número secreto?
| (a) 1 |
(b) 2 |
(c) 3 |
(d) 4 |
(e) 5 |
Ver la solución
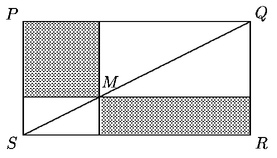
Problema 31. ¿Qué proporción guardan las
áreas de las dos regiones grises marcadas en el rectángulo
PQRS,
si M es un punto cualquiera de la diagonal?
 (Este problema forma parte delExamen Canguro
Animado)
(Este problema forma parte delExamen Canguro
Animado)
| (a) La de arriba es más grande |
(b) La de abajo es más grande |
(c) Son iguales |
(d) Sólo son iguales si M es el punto medio |
(e) No hay suficientes datos |
Ver la solución
Problema 32. De la ciudad A a la ciudad B hay
3 caminos, de la ciudad A a la ciudad C hay 5 caminos, de
la ciudad
B a la D hay 2 caminos y de la ciudad C
a la
D hay dos caminos. Si un camino que une dos ciudades no pasa
por otra, ¿cuántas formas hay de ir de la ciudad A
a la
D?
| (a) 12 |
(b) 16 |
(c) 19 |
(d) 32 |
(e) 60 |
Ver la solución
Problema 33. Se construyó un cubo de alambre de 3 cm
de lado dividido en 27 cubitos de 1 cm de lado cada uno. ¿Cuántos
centímetros de alambre se usaron para marcar las aristas de los
cubos (si no hubo desperdicio)?
(Este problema forma parte delExamen Canguro
Animado)
| (a) 25 |
(b) 64 |
(c) 72 |
(d) 120 |
(e) 144 |
Ver la solución
Problema 34. Un triángulo rectángulo tiene hipotenusa
6 y perímetro 14, ¿cuál es su área?
| (a) 3 |
(b) 7 |
(c) 10 |
(d) 14 |
(e) 28 |
Ver la solución
Problema 35. Alicia va al club cada día; Beatriz va cada
2 días; Carlos va cada 3; Daniel cada 4; Enrique cada 5; Francisco
cada 6 y Gabriela cada 7. Si hoy están todos en el club, ¿dentro
de cuántos días será la primera vez que vuelvan a
reunirse?
| (a) 27 |
(b) 28 |
(c) 210 |
(d) 420 |
(e) 5040 |
Ver la solución
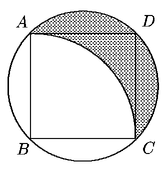
Problema 36. En la figura, cada lado del cuadrado mide 1. ¿Cuál
es el área de la región sombreada?
(a)  /2 /2 |
(b)  /4 /4 |
(c) 1/2 |
(d) 1 -  /4 /4 |
(e) 1 -  /2 /2 |
Problema 37. Dos enteros a>1 y b>1 satisfacen
ab+
ba=
57. Encuentra la suma a+b.
| (a) 5 |
(b) 7 |
(c) 10 |
(d) 12 |
(e) 57 |
Ver la solución
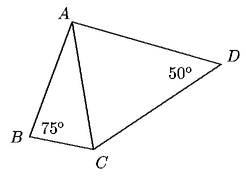
Problema 38. En la siguiente figura AD = DC, AB
= AC, el ángulo  ABC mide 75o y
el ángulo ABC mide 75o y
el ángulo  ADC mide 50o. ¿Cuánto
mide el ángulo ADC mide 50o. ¿Cuánto
mide el ángulo  BAD? BAD?
| (a) 30o |
(b) 85o |
(c) 95o |
(d) 125o |
(e) 140o |
Ver la solución
Problema 39. ¿Cuánto mide el área de la
parte sombreada?
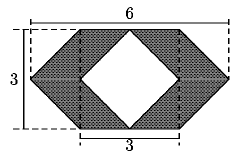 (Este problema forma parte delExamen Canguro
Animado)
(Este problema forma parte delExamen Canguro
Animado)
| (a) 9 |
(b)3/ |
(c) 18 |
(d) 12 |
(e)6/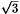 - -  |
Problema 40. El promedio de 5 números es 40. Al eliminar
dos de ellos el nuevo promedio es 36. ¿Cuál es el promedio
de los dos números eliminados?
| (a) 34 |
(b) 38 |
(c) 42 |
(d) 46 |
(e) 50 |
Ver la solución
Problema 41. Si cada letra C, A, N,
G,
U,
R,
O,
S,
corresponde a un dígito entonces
10,000 x UROS - 10,000 x CANG + CANGUROS
es igual a:
| (a) UROSUROS |
(b) UROSCANG |
(c) CANGCANG |
(d) CANGUROS |
(e) CARUNGOS |
Ver la solución
Problema 42. En el triángulo ABC, AB =
1,
BC = 2 y el ángulo  ABC
es de 72o. Se rota el triángulo ABC en el sentido
de las manecillas del reloj fijando el vértice B, obteniéndose
el triángulo A'BC'. Si A,B,C' son colineales y el arco AA'
es el descrito por A durante la rotación, ¿cuánto
vale el área sombreada? ABC
es de 72o. Se rota el triángulo ABC en el sentido
de las manecillas del reloj fijando el vértice B, obteniéndose
el triángulo A'BC'. Si A,B,C' son colineales y el arco AA'
es el descrito por A durante la rotación, ¿cuánto
vale el área sombreada?
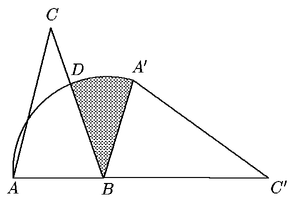 (Este problema forma parte delExamen Canguro
Animado)
(Este problema forma parte delExamen Canguro
Animado)
(a) /6 /6 |
(b) - 3/2 - 3/2 |
(c) /10 /10 |
(d)1 -  /2 /2 |
(e)3 /8 /8 |
Ver la solución
Problema 43. ¿Cuántos números múltiplos
de 6 menores que 1000 tienen la propiedad de que la suma de sus cifras
es 21?
| (a) 6 |
(b) 9 |
(c) 12 |
(d) 15 |
(e) 18 |
Ver la solución
Problema 44. Si xes un número par y yun
número impar, ¿cuál de los siguientes números
no es impar?
| (a) x+y |
(b) x+x+1 |
(c) x2/2 |
(d) (y+y)/2 |
(e) xy+1 |
Ver la solución
Problema 45. ¿Cuántos números entre 5678
y 9876 tienen la propiedad de que el producto de sus cifras es igual a
343?
| (a) 1 |
(b) 2 |
(c) 3 |
(d) 4 |
(e) 5 |
Ver la solución
Problema 46. Un barquillo de helado en Planilandia está
formado por un triángulo ABC equilátero (el barquillo)
y un círculo de radio 1 (la bola de nieve) tangente a AB
y AC. El centro del círculo O está en BC.
Cuando se derrite el helado se forma el triángulo AB'C' de
la misma área que el círculo y con BC y B'C'
paralelos. ¿Cuál es la altura del triángulo AB'C'?
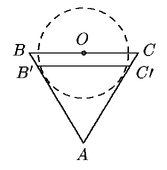
Ver la solución
Problema 47. Una mesa tiene un agujero circular con un diámetro
de 12 cm. Sobre el agujero hay una esfera de diámetro 20 cm. Si
la mesa tiene 30 cm de altura, ¿cuál es la distancia en centímetros
desde el punto más alto de la esfera hasta el piso?
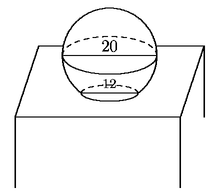
| (a) 40 cm |
(b) 42 cm |
(c) 45 cm |
(d) 48 cm |
(e) 50 cm |
Ver la solución
Problema 48. Un niño corta un cuadrado de tres días
por tres días de la página de un calendario. Si la suma de
las nueve fechas es divisible entre 10 y sabemos que la fecha de la esquina
superior izquierda es múltiplo de 4. ¿Cuál es la fecha
de la esquina inferior derecha?
| (a) 2 |
(b) 12 |
(c) 18 |
(d) 22 |
(e) 28 |
Ver la solución
Problema 49. Sea f una función de números
tal que
f(2)=3, y f(a+b)=f(a)+f(b)+ab,
para toda a y b. Entonces, f(11) es igual a:
| (a) 22 |
(b) 33 |
(c) 44 |
(d) 55 |
(e) 66 |
Ver la solución
Problema 50. ¿Cuál es el dígito de las
unidades de (1+12)+(2+22)+(3+32)+ ...
+(2000+20002)?
| (a) 0 |
(b) 2 |
(c) 4 |
(d) 6 |
(e) 8 |
Ver la solución
Inicio de la página
|















