|
Problema 1. Un pastel se corta quitando cada vez la tercera
parte del pastel que hay en el momento de cortar. ¿Qué fracción
del pastel original quedó después de cortar tres veces?
| (a) 2/3 |
(b) 4/3 |
(c) 4/9 |
(d) 8/9 |
(e) 8/27 |
Ver la solución
Problema 2. Un costal está lleno de canicas de 20 colores
distintos. Al azar se van sacando canicas del costal. ¿Cuál
es el mínimo número de canicas que deben sacarse para poder
garantizar que en la colección tomada habrá al menos 100
canicas del mismo color?
| (a) 1960 |
(b) 1977 |
(c) 1981 |
(d) 1995 |
(e) 2001 |
Ver la solución
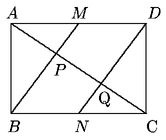
Problema 3. En el rectángulo de la figura, M y
N
son los puntos medios de AD y BC, respectivamente, y P
y Q son las respectivas intersecciones de AC con
BM
y con ND. Suponiendo que AD mide 5cm y que AB mide
3cm, ¿cuántos centímetros tiene de superficie el cuadrilátero
MPQD?
| (a) 2.75 |
(b) 3 |
(c) 3.25 |
(d) 3.75 |
(e) 4 |
Ver la solución
Problema 4. A una cantidad le sumo su 10%, y a la cantidad así
obtenida le resto su 10%. ¿Qué porcentaje de la cantidad
original me queda?
| (a) 98 |
(b) 99 |
(c) 100 |
(d) 101 |
(e) 102 |
Ver la solución
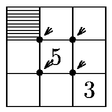
Problema 5. Dentro del cuadrado de la figura se escriben los
números enteros del 1 al 9 (sin repetir). La suma de los 4 números
alrededor de cada uno de los vértices marcados con flechas tiene
que ser 20. Los números 3 y 5 ya han sido escritos. ¿Qué
número debe ir en la casilla sombreada?
| (a) 1 |
(b) 2 |
(c) 4 |
(d) 7 |
(e) 9 |
Ver la solución
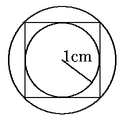
Problema 6. Un círculo cuyo radio mide 1 cm está
inscrito en un cuadrado, y éste a su vez está inscrito en
otro círculo, como se muestra en la figura. ¿Cuántos
centímetros mide el radio de éste último círculo?
Ver la solución
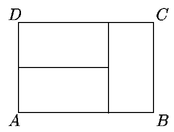
Problema 7. Con tres rectángulos iguales se formó
un rectángulo más grande, como el que se muestra en la figura.
Si la longitud
BC = 2, ¿Cuál es la longitud de AB?
| (a) 2.5 |
(b) 3 |
(c) 3.5 |
(d) 4 |
(e) 4.5 |
Ver la solución
Problema 8. La suma de tres números impares consecutivos
es igual a 27. ¿Cuál es el número más pequeño
de esos tres?
| (a) 11 |
(b) 9 |
(c) 8 |
(d) 7 |
(e) 5 |
Ver la solución
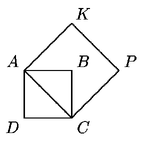
Problema 9. Cada lado del cuadrado ABCD mide 1
m. ¿Cuál
es el área del cuadrado AKPC?
| (a) 1 m2 |
(b) 1.5 m2 |
(c) 2 m2 |
(d) 2.5 m2 |
(e) 3 m2 |
Ver la solución
Problema 10. Utilizando cada una de las cifras 1, 2, 3 y 4 se
pueden escribir diferentes números, por ejemplo, podemos escribir
3241. ¿Cuál es la diferencia entre el más grande y
el más pequeño de los números que se construyen así?
| (a) 2203 |
(b) 2889 |
(c) 3003 |
(d) 3087 |
(e) 3333 |
Ver la solución
Problema 11. Si se dibujan un círculo y un
rectángulo
en la misma hoja, ¿cuál es el máximo número
de puntos comunes que pueden tener?
| (a) 2 |
(b) 4 |
(c) 5 |
(d) 6 |
(e) 8 |
Ver la solución
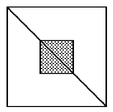
Problema 12. En la figura, el área del cuadrado de mayor
tamaño es igual a 1 m2. Una de sus diagonales se divide
en tres segmentos de la misma longitud. El segmento de enmedio es la diagonal
del pequeño cuadrado gris. ¿Cuál es el área
del cuadrado pequeño?
| (a) 1/10 m2 |
(b) 1/9 m2 |
(c) 1/6 m2 |
(d) 1/4 m2 |
(e) 1/3 m2 |
Ver la solución
Problema 13. 99 - 97 + 95 - 93 + ... +3 - 1 =
| (a) 48 |
(b) 64 |
(c) 32 |
(d) 50 |
(e) 0 |
Ver la solución
Problema 14. Una sala de cine tiene 26 filas con 24 asientos
cada una. El total de los asientos se numera de izquierda a derecha, comenzando
por la primera fila y hacia atrás. ¿En qué número
de fila está el asiento número 375?
| (a) 12 |
(b) 13 |
(c) 14 |
(d) 15 |
(e) 16 |
Ver la solución
Problema 15. El boleto de entrada al Palacio de las Ciencias
cuesta 5 pesos por niño y 10 pesos por adulto. Al final del día
50 personas visitaron el Palacio y el ingreso total de las entradas fue
de 350 pesos. ¿Cuántos adultos visitaron el Palacio?
| (a) 18 |
(b) 20 |
(c) 25 |
(d) 40 |
(e) 45 |
Ver la solución
Problema 16. A un cuadrado de papel se le cortan todas las
esquinas
¿Cuál es el máximo número de esquinas que puede
quedar?
| (a) 0 |
(b) 3 |
(c) 4 |
(d) 6 |
(e) 8 |
Ver la solución
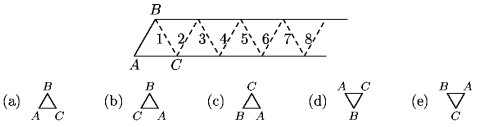
Problema 17. La figura representa una tira larga de papel
dividida
en 2001 triángulos marcados con líneas punteadas. Supongamos
que la tira será doblada siguiendo las líneas punteadas en
el orden indicado por los números, de forma que la tira siempre
quede en posición horizontal y la parte de la izquierda que ya ha
sido doblada se dobla hacia la derecha. ¿Cuál es la posición
en que terminan los vértices A,B,C después
de 1999 dobleces?
(Este problema forma parte delExamen Canguro Animado)
Ver la solución
Problema 18. Dos triángulos equiláteros iguales
se pegan por un lado. Después todas las esquinas de la figura obtenida
se juntan en el centro. ¿Qué figura se obtiene?
| (a) un triángulo |
(b) una estrella |
(c) un rectángulo |
(d) un hexágono |
(e) un rombo |
Ver la solución
Problema 19. El entrenador más experimentado del circo
necesita 40 minutos para lavar un elefante. Su hijo lleva a cabo la misma
tarea en 2 horas. ¿Cuántos minutos tardarán el entrenador
y su hijo en lavar 3 elefantes trabajando juntos?
| (a) 30 |
(b) 45 |
(c) 60 |
(d) 90 |
(e) 100 |
Ver la solución
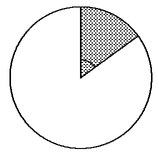
Problema 20. Me comí una rebanada de un pastel redondo
que representaba el 15 % del pastel, como indica la figura. ¿Cuál
es ángulo que abarca la rebanada del pastel?
| (a) 15o |
(b) 36o |
(c) 45o |
(d) 54o |
(e) 60o |
Ver la solución
Problema 21. Si 800 pesos tienen el mismo valor que 100 lipras
y 100 pesos tienen el mismo valor que 250 bólares, ¿cuántas
lipras valen lo mismo que 100 bólares?
| (a) 2 |
(b) 5 |
(c) 10 |
(d) 25 |
(e) 50 |
Ver la solución
Problema 22. Una acción en la bolsa de valores vale 1499
pesos en mayo. De mayo a junio la acción aumenta un 10 %. De junio
a julio la acción disminuye un 10 %. ¿Cuántos pesos
vale a fin de julio?
| (a) 1450 |
(b) 1400 |
(c) 1390 |
(d) 1386 |
(e) 1376 |
Ver la solución
Problema 23. Si efectuamos el producto de todos los
números
impares comprendidos entre 1 y 1994, ¿cuál es la cifra de
las unidades del número así obtenido?
| (a) 1 |
(b) 3 |
(c) 5 |
(d) 7 |
(e) 9 |
Ver la solución
Problema 24. ¿Qué dígitos hay que eliminar
en el número 4921508 para obtener el número de tres dígitos
más pequeño posible?
(Este problema forma parte delExamen Canguro Animado)
| (a) 4, 9, 2, 1 |
(b) 4, 2, 1, 0 |
(c) 1, 5, 0, 8 |
(d) 4, 9, 2, 5 |
(e) 4, 9, 5, 8 |
Ver la solución
Problema 25. En una tira de papel rectangular se dibujan
líneas
verticales que la dividen en 4 partes iguales. También se dibujan
líneas verticales que la dividen en 3 partes iguales. Finalmente,
se corta la tira siguiendo las las líneas dibujadas. ¿Cuántos
pedazos de diferente longitud se tienen?
| (a) 2 |
(b) 3 |
(c) 4 |
(d) 5 |
(e) 6 |
Ver la solución
Inicio de la página
|















