Problema 51. En una hoja de papel cuadriculado cada cuadrito
mide 1 x 1. Se coloca una moneda de diámetro  ? encima.
¿Cuál es el máximo número de cuadritos que
puede cubrir parcialmente (de manera que la región cubierta en ese
cuadrito tenga área mayor que 0) la moneda? ? encima.
¿Cuál es el máximo número de cuadritos que
puede cubrir parcialmente (de manera que la región cubierta en ese
cuadrito tenga área mayor que 0) la moneda?
| (a) 4 |
(b) 5 |
(c) 6 |
(d) 7 |
(e) 8 |
Ver la solución
Problema 52. Yo salí de mi casa en automóvil a
las 8:00 de la mañana. Un automóvil que va al doble de mi
velocidad sale también de mi casa, me alcanza exactamente a la mitad
del camino y llega 1:30h antes que yo a nuestro lugar de destino. ¿A
qué hora salió el otro automóvil?
| (a) 8:00 h |
(b) 8:30 h |
(c) 9:00 h |
(d) 9:30 h |
(e) 10:00 h |
Ver la solución
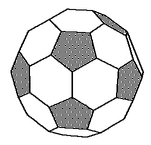
Problema 53. Un poliedro en forma de balón de futbol
tiene 32 caras: 20 son hexágonos regulares y 12 son pentágonos
regulares. ¿Cuántos vértices tiene el poliedro?
| (a) 72 |
(b) 90 |
(c) 60 |
(d) 56 |
(e) 54 |
Ver la solución
Problema 54. Dadas cuatro líneas diferentes, ¿cuántos
puntos de intersección NO puede haber entre ellas?
| (a) 0 |
(b) 2 |
(c) 3 |
(d) 5 |
(e) 6 |
Ver la solución
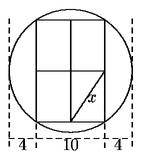
Problema 55. ¿Cuál es la longitud de x
en la figura?
 (Este problema forma parte delExamen Canguro
Animado)
(Este problema forma parte delExamen Canguro
Animado)
(a)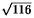 |
(b)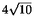 |
(c) 9 |
(d) 12 |
(e) 18 |
Ver la solución
Problema 56. Si S = 1 + 2 + 3 +
...
+ 100, ¿cuántos signos + hay que cambiar
por signos
- para obtener 1991 en lugar de S?
| (a) Es imposible |
(b) 3 |
(c)4 |
(d) 5 |
(e) 6 |
Ver la solución
Problema 57. Cinco amigos P,Q,R,S
y T se dan la mano. Tanto P como Q estrecharon la
mano de uno solo de sus amigos, mientras que R, S y T
estrecharon cada uno la mano de dos. Sabemos que P estrechó
la mano de
T. ¿Quiénes podemos asegurar que no se
dieron la mano?
| (a) T y S |
(b) T y R |
(c) Q y R |
(d) Q y T |
(e) Q y S |
Ver la solución
Problema 58. En un concurso de baile los jueces califican a
los competidores con números enteros. El promedio de las calificaciones
de un competidor es 5.625 ¿Cuál es el número mínimo
de jueces para que eso sea posible?
| (a) 2 |
(b) 6 |
(c) 8 |
(d) 10 |
(e) 12 |
Ver la solución
Problema 59. Una caja que compró mamá está
llena de chocolates en forma de cubo. Sara se comió todos los del
piso de arriba, que eran 77. Después se comió 55, que eran
los que quedaban en un costado. Después se comió los que
quedaban enfrente. Sobraron algunos chocolates en la caja; ¿cuántos?
| (a) 203 |
(b) 256 |
(c) 295 |
(d) 300 |
(e) 350 |
Ver la solución
Problema 60. La maestra distribuyó la misma cantidad
de dulces entre cada uno de 5 niños y se quedó tres para
ella misma. No se acuerda cuántos dulces tenía, pero se acuerda
que era un múltiplo de 6 entre 65 y 100. ¿Cuántos
dulces tenía?
| (a) 63 |
(b) 78 |
(c) 90 |
(d) 93 |
(e) 98 |
Ver la solución
Problema 61. Las siguientes figuras consisten en cubitos desdoblados.
¿Cuál de ellas corresponde a un cubo en el que cada dos regiones
triangulares que comparten una arista son del mismo color?

Ver la solución
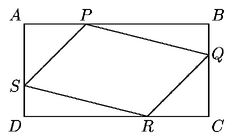
Problema 62. En la figura los puntos P,Q,R
y S y T dividen cada lado del rectángulo en razón
1:2.
¿Cuál es el cociente entre el área del paralelogramo
PQRS
y el área de ABCD?
 (Este problema forma parte delExamen Canguro
Animado)
(Este problema forma parte delExamen Canguro
Animado)
| (a) 2/5 |
(b) 3/5 |
(c) 4/9 |
(d) 5/9 |
(e) 2/3 |
Ver la solución
Problema 63. Consideremos 48 canicas repartidas en tres montones
A,
B
y C de manera que si del montón A pasamos al B
tantas canicas como hay en el B, luego del B pasamos al C
tantas canicas como hay en el C y del C pasamos al A
tantas como existen ahora en el A, tendremos el mismo número
de canicas en cada montón. ¿Cuántas canicas había
al principio en el montón A?
| (a) 16 |
(b) 19 |
(c) 20 |
(d) 22 |
(e) 30 |
Ver la solución
Problema 64. El producto de tres enteros positivos es 1500 y
su suma es 45. ¿Cuál es el mayor de esos tres números?
| (a) 27 |
(b) 28 |
(c) 29 |
(d) 30 |
(e) 31 |
Ver la solución
Problema 65. Se tienen dos círculos con centro en el
mismo punto, pero cuyos perímetros difieren en 1 cm. ¿cuál
es la diferencia entre sus radios?
(a)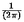
|
(b)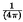
|
(c) cm cm |
(d)2 cm cm |
(e)4 cm cm |
Ver la solución
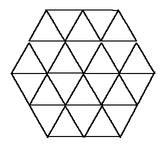
Problema 66. Un zoológico tiene forma hexagonal con celdas
que son triángulos equiláteros de lado 10, como en la figura.
En este zoológico se quieren poner 1000 animales salvajes; por seguridad
no puede haber dos animales en una misma celda y si una celda está
ocupada ninguna de las que comparte un lado con ella puede estarlo. ¿Cuánto
mide el lado del hexágono más chico que tiene esta propiedad?
| (a) 13 |
(b) 16 |
(c) 19 |
(d) 22 |
(e) 25 |
Ver la solución
Problema 67. Se escriben en sucesión todos los números
del 1 al 2001, en orden, uno a continuación del otro, para formar
un número muy grande que llamaremos G (es decir, G=1234567891011
... 20002001) ¿Cuál es la cifra central de G?
| (a) 1 |
(b) 3 |
(c) 5 |
(d) 7 |
(e) 9 |
Ver la solución
Problema 68. La siguiente figura se forma a partir de un triángulo
equilátero de área 1 prolongando cada lado dos veces su longitud
en ambas direcciones. El área de esta figura es:
| (a) 31 |
(b) 36 |
(c) 37 |
(d) 41 |
(e) 42 |
Ver la solución
Problema 69. El resultado de la operación siguiente:
1-2-3+4+5-6-7+8+ ... -1998-1999+2000 es
(a)
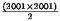
|
(b)
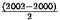
|
(c) 2001 |
(d) 0 |
(e) 2 |
Ver la solución
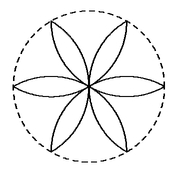
Problema 70. Una flor se ha dibujado dentro de un círculo
manteniendo la misma apertura del compás, como se muestra en la
figura. Si el perímetro de la flor es 2, ¿cuál es
el radio del círculo?
 (Este problema forma parte delExamen Canguro
Animado)
(Este problema forma parte delExamen Canguro
Animado)
(a)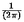
|
(b)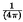
|
(c)1/6 |
(d)2 /3 /3 |
(e) /8 /8 |
Ver la solución
Problema 71. ¿Cuántas parejas de enteros positivos
(a,b)
satisfacen a2-b2=15?
| (a) 0 |
(b) 1 |
(c) 2 |
(d) 3 |
(e) 4 |
Ver la solución
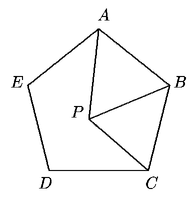
Problema 72. En la figura, ABCDE representa un pentágono
regular (de 1 cm de lado) y ABP es un triángulo equilátero.
¿Cuántos grados mide el ángulo  BCP? BCP?
| (a) 45o |
(b) 54o |
(c) 60o |
(d) 66o |
(e) 72o |
Ver la solucçión
Problema 73. El número -1 es solución de
la ecuación de segundo grado 3x2+bx+c=0. Si los
coeficientes b y c son números primos, el valor de
3c-b
es:
| (a) 0 |
(b) 1 |
(c) 2 |
(d) 3 |
(e) 4 |
Ver la solución
Problema 74. Una sucesión se forma de la manera siguiente:
el primer término es 2 y cada uno de los términos siguientes
se obtiene del anterior elevándolo al cuadrado y restando 1 (los
primeros términos son 2,22-1=3, 32-1=8, 82-1=63,
... ). La cantidad de números primos que hay en la sucesión
es:
| (a) 1 |
(b) 2 |
(c) 3 |
(d) 5 |
(e) infinita |
Ver la solución
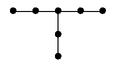
Problema 75. El número de triángulos con sus tres
vértices en los puntos de la figura es:
| (a) 20 |
(b) 24 |
(c) 28 |
(d) 32 |
(e) 36 |
Ver la solución
Inicio de la página
|








 ? encima.
¿Cuál es el máximo número de cuadritos que
puede cubrir parcialmente (de manera que la región cubierta en ese
cuadrito tenga área mayor que 0) la moneda?
? encima.
¿Cuál es el máximo número de cuadritos que
puede cubrir parcialmente (de manera que la región cubierta en ese
cuadrito tenga área mayor que 0) la moneda?







