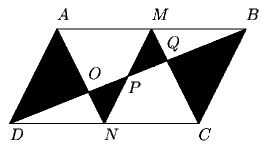
Solución 76.
Si XYZ es un triángulo, denotemos su área como
(XYZ).
El triángulo ADO es semejante al triángulo
ONP
en razón 1:2, así OD=2OP. Como los triángulos
ODN
y ONP comparten la altura trazada desde el vértice
N,
entonces (ONP) = 1/2 (ODN). Por el mismo argumento 1/2 (ODN)=(ADO).
Luego entonces (ADO) + (ONP)= 5/6 (ADN) = 5/6(1/4)
= 5/24.Análogamente el área de la región sombreada
en el paralelogramo MBCN también es 5/24, y el total del
área sombreada es 2(5/24)=5/12. La respuesta es (c).
Regresar al problema
Solución 77.
Llamemos a los ciclistas A y B. Si el ciclista A
se encuentra con el ciclista B en la primera esquina a la que llega
una vez iniciado su recorrido, significa que B recorrió tres
lados del cuadrado mientras A recorrió uno, y la razón
entre sus velocidades es 1:3. Si se encuentran en la segunda esquina
a partir de que A inició su recorrido, entonces la velocidad
de A es la misma que la de B (recorrieron la misma distancia
en el mismo tiempo), pero la tercera vez se encontrarían en la misma
esquina donde empezaron, lo cual no puede ser. Por el mismo razonamiento
del primer caso, si se encuentran en la tercera esquina a la que llegó
A,
la razón entre sus velocidades es 1:3. La respuesta es (b).
Regresar al problema
Solución 78.
Como se comió los dulces de 3 en 3, sólo pueden quedar
dulces de aquéllos de los que originalmente no había una
cantidad múltiplo de 3: los verdes. La respuesta es (d).
Regresar al problema
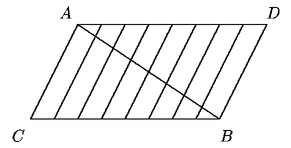
Solución 79.
Tracemos por A una paralela a BC y por B una paralela
a AC. Si D es su punto de intersección, cada uno de
los segmentos paralelos a AC que se han dibujado son del mismo tamaño.
La suma de las longitudes de los segmentos paralelos dentro del triángulo
ABC
es igual a la suma de las longitudes de los segmentos paralelos dentro
del triángulo ABD. Así, la suma de los segmentos en
un solo triángulo es igual a (7x10)/2 = 35. La respuesta es (d).
Regresar al problema
Solución 80.
El perímetro del cuadrado redondeado es 4 x 2 + (4 x 2 + (4 x 2 x 2/4) = 12 x 2/4) = 12 , y esto es es 6 veces el perimetro de la rueda, que es
de 2 , y esto es es 6 veces el perimetro de la rueda, que es
de 2 . La respuesta es (b). . La respuesta es (b).
Regresar al problema
Solución 81.
Cada vez que se concede un deseo el pedazo de piel se reduce a 1/6
de su área. Después de conceder 3 deseos, el pedazo de piel
tiene un área de 1/6 x 1/6 x 1/6 = 1/216 veces el área original.
Al principio, el pedazo de piel tenía un área de 4 x 216=864
cm2, y como se trataba de un rectángulo donde una arista
medía 9 cm, la otra medía 96 cm. La respuesta es (b).
Regresar al problema
Solución 82.
Observemos que 96 = 25 x 3. Entonces los únicos divisores
de 96 que están entre 5 y 20 son 2 x 3 = 6, 22 x 3=12,
23=8 y 24=16. Por lo tanto sólo podemos hacer
equipos de cuatro maneras diferentes. La respuesta es (d).
Regresar al problema
Solución 83.
Dividir 1 entre 52000 es lo mismo que calcular (1/ 5)2000
= (0.2)^2000. Al elevar 0.2 a alguna potencia, observemos el
comportamiento de su última cifra:
(0.2)1 = ... 2
(0.2)2 = ... 4
(0.2)3 = ... 8
(0.2)4 = ... 6
(0.2)5 = ... 2
.
.
.
La secuencia se repite en lo sucesivo cada 4 números y, como
2000 es múltiplo de 4, es fácil observar que la última
cifra no cero en la división será 6. La respuesta es (c).
Regresar al problema
Solución 84.
Tenemos que
415 = (22)15 = 230
811 = (23)11 = 233
168 = (24)8 = 232
326 = (25)6 = 230
El más grande es 811. La respuesta es (c).
Regresar al problema
Solución 85.
Agrupemos todos los 2's y los 5's que podamos:21998
x 52002=(2 x 5)1998 x 54=625 x 101998.
La respuesta es (c).
Regresar al problema
Solución 86.
De la A a la Z, en orden, hay 26 letras, así que
de AAA a AAZ hay 26 códigos (AAZ es el número
26). De la misma manera, de AAA a AZZ hay 26 x 26 = 676 códigos.
Podemos ver que 2203 = 676 x 3 + 175, así que aún nos faltan
175 códigos después de CZZ, que es el código
3 x 26 x 26 = 2028. Como 175 = 6 x 26 + 19, después de DFZ
(que es el código 626 + 26 x 6) nos faltan aún 19 códigos,
así que la etiqueta es DGS. La respuesta es (c).
Regresar al problema
Solución 87.
La sucesión de flechas es periódica y se repite cada
6 números. Tenemos que 1997 = (6 ... 332) + 5, así es que
la sucesión de 1997 a 2000 es la misma que de 5 a 8. La respuesta
es (e).
Regresar al problema
Solución 88.
Para un triángulo XYZ, denotemos su área por (XYZ).
Tenemos entonces que
(BAP) / (BCP) = AP x h / PC x h
= AP / PC
(DAP) / (CDP) = AP x h / PC x h
= AP / PC
(DAP) / (CDP) = (BAP) / (BCP), de donde
(BAP) / 120 = 300 / 200 y
(BAP) = 180
La respuesta es (b).
Regresar al problema
Solución 89.
Observemos que los lados de los triángulos que se forman al
tomar tres vértices, sólo pueden ser aristas del cubo, diagonales
de alguna cara o diagonales del cubo. Es fácil observar que todos
los triángulos que tienen a una diagonal del cubo como uno de sus
lados son rectángulos (y por lo tanto no son equiláteros).
Por otra parte, los triángulos quetienen aristas como dos de sus
lados (a partir del mismo vértice) también son rectángulos.
Fijándonos ahora en las diagonales de caras,observemos que los únicos
triángulos equiláteros se forman con las diagonales de tres
caras que coinciden en un vértice y que no pasan por él,
y habrá tantos triángulos equiláteros como vértices
tiene el cubo: ocho. La respuesta es (b).
Regresar al problema
Solución 90.
Como a+f+d es par, y b+f+d es par también, tenemos
que a y b son los dos pares o los dos impares. Usando el
mismo argumento, llegamos a que a,b,c,d y e tienen la misma
paridad. Así f tiene que ser par, puesto que a+d es par
(suma de dos pares o de dos impares). Luego a,b,c,d y e tienen
que ser impares porque la suma de las áreas es 31. Entonces a,b,c,d
y e son los números del 1 al 9 en algún orden, y f=31-1-3-5-7-9=6.
La respuesta es (d).
Regresar al problema
Solución 91.
Los triángulo ABT y ARO son semejantes en razón
2:1
pues O es el punto medio de AT, y RO es paralela a
BT;
así, como en el triángulo ARO los lados
AO
y RO son iguales, también lo son sus correspondientes en
el triángulo ABT, es decir, BT=AT; por tanto
BT=3.
El área buscada es: área (ABT) - área
(ARO)
- 1/4 área (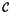 = 3 x 3/2 - (3/2 x(3/2)/2) - 1 = 3 x 3/2 - (3/2 x(3/2)/2) - 1 /4 x (3/2)2=27/8-9 /4 x (3/2)2=27/8-9 /16.
La respuesta es (e) . /16.
La respuesta es (e) .
Regresar al problema
Solución 92.
El triángulo ABC es isósceles y  ABC= ABC=
 ACB. Como el triángulo BCD es isósceles
también, ACB. Como el triángulo BCD es isósceles
también,  ABD= ABD=  BDA. Como BCD
es isósceles también, y usando que la suma de los ángulos
internos de un triángulo es 180o, tenemos BDA. Como BCD
es isósceles también, y usando que la suma de los ángulos
internos de un triángulo es 180o, tenemos  BCD= BCD=  BDC=180o-BDA= BDC=180o-BDA=  ABD + ABD +  BAD= 2 BAD= 2  ABD. Luego 5 ABD. Luego 5 ABD= 180o y ABD= 180o y  ABD=36o. La respuesta es (b). ABD=36o. La respuesta es (b).
Regresar al problema
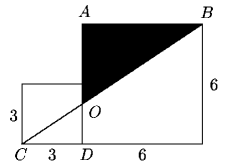
Solución 93.
Observemos que el triángulo ABO es semejante al triángulo
DCO
en razón 2:1 (AB=2CD). Entonces
AO=2DO,
pero como AO+DO=6, tenemos que AO=4. Por lo tanto
el área del triángulo sombreado es (AB x AO)/2=
6 x 4/2=12. La respuesta es (c).
Regresar al problema
Solución 94.
Si alguno de los números que salen (o en el dado o en la moneda)
es par, el resultado es par. Hay probabilidad de 1/2 de que salga el 2
en la moneda, y la probabilidad de que si salga 1 en la moneda y un número
par en el dado es de 1/2 x 1/2 = 1/4. Así, la probabilidad de que
gane Edgar es 1/2 + 1/4 = 3/4. La respuesta es (c).
Regresar al problema
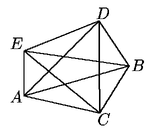
Solución 95.
Representemos cada camino como una cadena deletras. Así, el
camino ACEDB es el que recorre los segmentos AC, CE,
ED
y DB. Todas las cadenas deben empezar en A y terminar en
B,
y tienen a lo más 5 letras (no se puede pasar por el mismo vértice
dos veces). Hay una sola cadena de dos letras que representa un camino
válido: AB. Hay 3 cadenas de tres letras que representan
caminos válidos: ACB, ADB, AEB. Los caminos
que pasan por cuatro vértices son de la forma A _ _ B, donde
hay 6 opciones para poner en lugar de las líneas:
CD, DE,
CE,
DC,
ED
y EC. Por la misma razón, pasando por los cinco vértices
hay tantos caminos como cadenas diferentes con tres letras distintas: CED,
CED,
EDC,
ECD,
DEC
y
DCE. En total son 1+3+6+6=16 formas. La respuesta es (c).
Regresar al problema
Solución 96.
Tenemos que (x+y)2=x2+2xy+y2=8xy,
así que, despejando, x+y=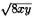 . De la misma manera, de (x-y)2=x2-2xy+y2=4xy
obtenemos x+y= . De la misma manera, de (x-y)2=x2-2xy+y2=4xy
obtenemos x+y=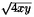 . Entonces (x+y)/(x-y)= . Entonces (x+y)/(x-y)=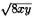 / /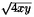 = =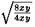 = = .
La respuesta es (c). .
La respuesta es (c).
Regresar al problema
Solución 97.
Tenemos que BE=1 - EC, FC=EC y AE=2EF.
Aplicando el Teorema de Pitágoras en EFC obtenemos EF2=EC2+EC2,
de donde EC=(1/ )EF. Apliquemos el Teorema de Pitágoras al triángulo ABE
y sustituyamos el valor de EC que acabamos de obtener: )EF. Apliquemos el Teorema de Pitágoras al triángulo ABE
y sustituyamos el valor de EC que acabamos de obtener:
(2EF)2 = 1+(1-EC)2
4EF2 = 1+1- 2EC+EC2 = 2-2EC+EC2
=
2-2((1/ )EF)+1/2 x EF2 )EF)+1/2 x EF2
7/2EF2+ EF-2= 0 EF-2= 0
Resolviendo obtenemos EF =1/7(-  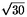 ). Como
EF
es una longitud, tomamos el valor positivo en la raíz y, por lo
tanto EF=1/7(- ). Como
EF
es una longitud, tomamos el valor positivo en la raíz y, por lo
tanto EF=1/7(- + +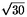 ). La respuesta es (c). ). La respuesta es (c).
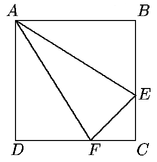
Regresar al problema
Solución 98.
Los tres arcos fueron trazados con el mismo radio, luego el triángulo
ABC
es equilátero de lado 1. Como en el triángulo equilátero
todos los ángulos son iguales a 60o entonces tenemos
que el área del sector CB es una sexta parte del área
del círculo, es decir, ( r2)/6= r2)/6= /6; análogamente
las áreas de los sectores AB y AC son /6; análogamente
las áreas de los sectores AB y AC son  /6, respectivamente.
El área de la figura es la suma del área de los tres sectores
menos dos veces el área del triángulo ABC. La altura
del triángulo ABC es /6, respectivamente.
El área de la figura es la suma del área de los tres sectores
menos dos veces el área del triángulo ABC. La altura
del triángulo ABC es 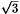 /2, entonces su área
es bh/2=(1 x ( /2, entonces su área
es bh/2=(1 x (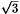 /2)/2= /2)/2=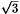 /4 Por lo tanto,
el área de la figura es: A=3( /4 Por lo tanto,
el área de la figura es: A=3( /6)-2( /6)-2(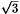 /over4)=( /over4)=( - -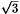 )/2. La respuesta es (d). )/2. La respuesta es (d).
Regresar al problema
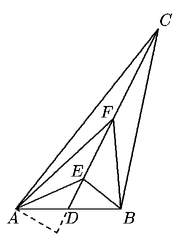
Solución 99.
El área del triángulo ADE es 1. La altura trazada
desde el vértice A de los triángulos ADE y
AEF
es la misma, pero la base del triángulo AEF es el doble de
la base del triángulo ADE, por lo tanto, el área del
triángulo AEF es 2.
Análogamente, la altura del triángulo ADE es igual
a la altura del triángulo AFC y, como la base del triángulo
AFC
es el triple de la base del triángulo ADE, el área
del triángulo AFC es 3. El área del triángulo
DBE
es igual al área del triángulo ADE ya que tienen la
misma base y la misma altura. De la misma manera que en los casos anteriores,
las áreas de los triángulos BEF y BFC son el
doble y el triple, respectivamente, del área del triángulo
BDE;
entonces tenemos que el área del triángulo ABC=2 x
1+2 x 2+2 x 3=12. La respuesta es (e).
Regresar al problema
Solución 100.
Sumando las dos últimas ecuaciones obtenemos 2x2=8,
de donde x=2. Sumando la primera y tercera ecuaciones tenemos que
2x2+2z=9. Sustituyendo el valor de x y
despejando llegamos a z=3. Sustituyendo x y z en la
segunda ecuación, tenemos que y=1/2. Por lo tanto xyz=3.
La respuesta es (d).
Regresar al problema
Inicio de la página
|













