Solución 51.
Observemos que  <2, así que la moneda toca a lo
más 3 cuadros horizontales y 3 verticales. Entonces el problema
se reduce a considerar una cuadrícula de 3 x 3. Si la moneda cubre
un pedazo de algún cuadro de la esquina, entonces no cubre el de
la esquina contraria porque la mínima distancia entre las dos esquinas
opuestas es <2, así que la moneda toca a lo
más 3 cuadros horizontales y 3 verticales. Entonces el problema
se reduce a considerar una cuadrícula de 3 x 3. Si la moneda cubre
un pedazo de algún cuadro de la esquina, entonces no cubre el de
la esquina contraria porque la mínima distancia entre las dos esquinas
opuestas es  (la diagonal del cuadrado). Son 4 esquinas, entonces
hasta ahora hemos visto que a lo más la moneda cubre 7 cuadritos.
Ahora veamos que sí es posible lograr cubrir 7 cuadritos. Para esto
observemos que si colocamos la moneda circunscribiendo el cuadro central,
entonces cubrirá (parcialmente) 5 cuadros; la recorremos hacia arriba
un poco (menos de (la diagonal del cuadrado). Son 4 esquinas, entonces
hasta ahora hemos visto que a lo más la moneda cubre 7 cuadritos.
Ahora veamos que sí es posible lograr cubrir 7 cuadritos. Para esto
observemos que si colocamos la moneda circunscribiendo el cuadro central,
entonces cubrirá (parcialmente) 5 cuadros; la recorremos hacia arriba
un poco (menos de  /2)para lograr que cubra todos los cuadros
salvo las esquinas inferiores. La respuesta es (d). /2)para lograr que cubra todos los cuadros
salvo las esquinas inferiores. La respuesta es (d).
Regresar al problema
Solución 52.
En vista de que a medio camino estábamos en el mismo lugar,
de que las velocidades fueron constantes y de que el otro automóvil
llegó 1h antes, entonces también salió 1:30h después:
a las 9:30 de la mañana. La respuesta es (d).
Regresar al problema
Solución 53.
Observemos que cada vértice lo es de cada pentágono y
que dos pentágonos no comparten ningun vértice. Como son
12 pentágonos y cada uno tiene 5 vértices, en total hay 60
vértices. (De otra manera: Hay 20 hexágonos, cada uno con
6 vértices, para un total de 120 vértices. Hay 12 pentágonos,
cada uno con 5 vértices, para un total de 60 vértices. Pero
cada vértice es compartido por tres figuras, por lo tanto el poliedro
tiene (120+60)/3 = 60 vértices.) La respuesta es (c).
Regresar al problema
Solución 54.
Por el enunciado sabemos que sólo una de las respuestas es imposible,
así es que basta dar un ejemplo de los casos que sí son posibles:
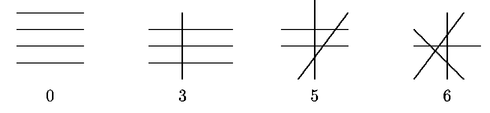 La respuesta es (b).
La respuesta es (b).
Regresar al problema
Solución 55.
Tenemos que x es la longitud de la diagonal de un rectángulo.
La otra diagonal del mismo rectángulo es un radio del círculo.
Como el diámetro del círculo mide 10 + 4 + 4 = 18, tenemos
que x mide 9. La respuesta es (c).
Regresar al problema
Solución 56.
Del 1 al 100 hay 50 números impares que, sumados a los otros
50 números pares, dan un número par. Si cambiamos un signo
+
por uno -, por ejemplo si escribimos - 5 en lugar de +
5, le estamos restando 10 a S; es decir, si escribimos
-
n en lugar de + n, en realidad le estamos restando 2n
a S. Pero, tanto S como 2n son pares, por lo tanto
S
- 2n es número par siempre. Entonces no es posible obtener
1991 de esta manera. La respuesta es (a).
Regresar al problema
Solución 57.
Si Q le hubiera dado la mano a T, entonces ni P
ni Q ni T le hubieran dado la mano a nadie más, lo
cual no es posible pues R le dio la mano a dos amigos. La respuesta
es (d).
Regresar al problema
Solución 58.
Observemos que 5.625 = 5625/1000 = 45/8, que es una fracción
simplificada y, por lo tanto, tenemos que multiplicar por 8 para poder
obtener un entero que sea la suma de las calificaciones de los jueces.
La respuesta es (c).
Regresar al problema
Solución 59.
Como el número de chocolates del piso de arriba es 77, la cantidad
de chocolates a lo largo por la cantidad de chocolates a lo ancho es 77.
Las posibilidades son 11 a lo largo y 7 a lo ancho, o 77 a lo largo, en
una sola hilera. Como al final quedan chocolates en la caja, la posibilidad
correcta es la primera: 11 x 7. Como después de comerse el piso
de arriba quedan 55 en un costado, cuando la caja estaba llena debió
tener 6 chocolates a lo alto. Así, inicialmente había 7 x
6 x 11 = 462 chocolates. Originalmente en el frente de la caja había
7 x 6=42 chocolates, de los cuales Sara se comió primero 7 de la
fila de arriba y 5 que quedaban en la fila de un costado. Quedan 462 -
77 - 55 - 30 = 300 chocolates. La respuesta es (d).
Regresar al problema
Solución 60.
Como se quedó con 3 dulces, el número inicial de dulces
termina en 3 o en 8, pero como es un múltiplo de 6, es par, por
lo que termina en 8. La única posibilidad es 78. La respuesta es
(b).
Regresar al problema
Solución 61.
Doblando dos cuadrados que tengan las regiones inmediatas a una misma
arista del mismo color, nos damos cuenta de que necesitamos que los vértices
en que esas aristas convergen tengan todas las regiones que incluyen a
esa arista del mismo color. Cada arista tiene tres regiones cercanas, por
lo cual el número de regiones de cada color debe ser divisible entre
tres. Solamente a) y d) cumplen con este requisito, y es fácil darse
cuenta de que al doblar a) hay varias aristas que no comparten regiones
del mismo color. La respuesta es (d).
Regresar al problema
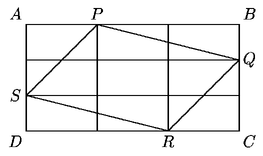
Solución 62.
Dibujamos paralelas al lado AD por P y R y también
al lado AB por S y Q. Cada uno de los rectángulos
pequeños representa 1/9 del área original. El área
de los triángulos rectángulos que tienen como cateto un lado
del rectángulo PQRS es un 1/9 del área de ABCD.
Así, el área de PQRS es 1/9 + 4/9 = 5/9 del área
de ABCD. La respuesta es (d).
Regresar al problema
Solución 63.
Cada montón, al final, tenía 16 canicas (en total había
48 y cadauno tenía el mismo número de canicas). El montón
A
tenía 16 canicas y, como del C pasamos al A tantas
canicas como éste tenía, el A tenía 8 y le
pasamos 8 canicas del C, luego el C tenía 16+8=24
canicas. Del B pasamos al C tantas canicas como había
en el C, entonces pasamos 24/2=12 canicas del B al C,
y el B tenía 16+12=28 canicas. Por último, del A
pasamos al $B$ tantas canicas como éste tenía, entonces pasamos
28/2=14 canicas del A al B, luego el A tenía
14+8=22 canicas. Por lo tanto, había al principio 22 canicas en
el montón A. La respuesta es (d).
Regresar al problema
Solución 64.
Observemos que 1500=22 x 53 x 3. Tenemos que
repartir los tres 5's que aparecen en la factorización de
1500 entre los tres números que buscamos. Es claro que los tres
no pueden quedar en un mismo número pues 53 = 125 > 45.
Entonces, por lo menos dos de los números son múltiplos de
5; pero el tercero es la diferencia de 45, que es múltiplo de 5,
y la suma de los otros dos números también lo es; así,
también ese número debe ser múltiplo de 5. Ahora ya
sólo tenemos que repartir los dos 2's y el 3, buscando que
la suma sea 45. Probando todas las posibilidades vemos que la única
es que los números sean 30, 10 y 5. La respuesta es (d).
Regresar al problema
Solución 65.
Si r el radio de la circunferencia más pequeña
y R el de la más grande, tenemos que 2 r + 1 = 2 r + 1 = 2 R,
y por lo tanto R-r =1/2 R,
y por lo tanto R-r =1/2 . La respuesta es (a). . La respuesta es (a).
Regresar al problema
Solución 66.
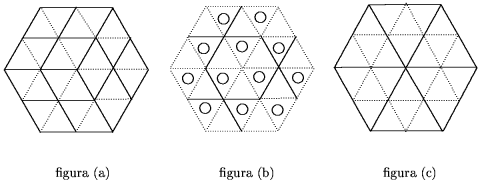
Si agrupamos las celdas por parejas según vértices vecinos
como se muestra en la figura (a), sabemos que en cada pareja una celda
está ocupada y la otra no. Así, cuando más, puede
usarse la mitad de las celdas del zoológico para acomodar a todos
los animales y, por lo tanto, necesitaremos al menos 2000 celdas para acomodarlos.
La figura (b) muestra cómo es posible acomodar animales en un zoológico
hexagonal utilizando la mitad de las celdas. Es fácil observar que
en un triángulo equilátero de lado n hay n2
triángulos de lado 1. Un hexágono regular está compuesto
por 6 triángulos equiláteros, como se muestra en la figura
(c). Como un hexágono de lado n tiene 6n2 celdas
tenemos que 6n2  2000, por lo cual necesitamos
n 2000, por lo cual necesitamos
n  19, así que 19 es suficiente. La respuesta es (c). 19, así que 19 es suficiente. La respuesta es (c).
Solución 67.
El número total de cifras de G es
9+2(99-9)+3(999-99)+4(2001-999)=9+180+2700+3990=6879.
Entonces la cifra central está en el lugar 3440. Para llegar
a esa cifra necesitamos todos los números del 1 al 999 (pues 9+180+2700=2889)
y otras 551 cifras más. Como a partir del 1000 todos los números
que se escriben tienen 4 cifras y 137 x 4=548, necesitaremos 137 números
después del 999 y 3 cifras más, es decir, la tercera cifra
que se escriba después de 1136, que es el 3 de 1137. La respuesta
es (b).
Regresar al problema
Solución 68.
El triángulo ABC es semejante al triángulo CEF
en razón 1:2, y por lo tanto el área de CEF
es 4 (la base y la altura miden el doble que las de CEF). De la
misma manera el triángulo ABC es semejante al triángulo
ADE
en razón 1:3, y el área de ADE es 9. Entonces,
el área de la figura es (9-1) x 3+ (4 x 3)+1 = 37. La respuesta
es (c).
Regresar al problema
Solución 69.
Reagrupemos los sumandos de la siguiente manera: ((1 - 2) + (5 - 6)
+ ... + (1997 - 1998)) + ((-3 + 4) + (-7 + 8) + ... + (-1999+2000))= (1)
x 500 + (-1) x 500 = 0. La respuesta es (d).
Regresar al problema
Solución 70.
Llamemos r al radio. Cada uno de los 6 arcos dibujados mide
1/3 del perímetro del círculo; entonces r satisface
6 x 1/3 /x 2 r = 2. La respuesta es (a) r = 2. La respuesta es (a)
Regresar al problema
Solución 71.
Como a y b son enteros positivos y (a+b)(a-b)=15,
entonces (a+b) es un entero positivo, (a-b) también
lo es, y (a+b)>(a-b). Hay dos posibilidades: (a-b)=1 y (a+b)=15
o (a+b)=3 y (a-b)=5. Si (a-b)=1 y (a+b)=15
tenemos que a=8 y b=7. Si (a-b)=3 y (a+b)=5
tenemos que a=4 y b=1. Entonces solamente hay 2 parejas de
enteros positivos que cumplen la ecuación. La respuesta es (c).
Regresar al problema
Solución 72.
Utilizaremos varias veces el resultado de que la suma de los ángulos
internos de un triángulo es 180o. Todos los ángulos
del pentágono miden (180o x 5 - 360o)/5=108o.
Entonces  PBC=48o. PBC=48o.
Observemos que PBC es un triángulo isósceles,
luego  BCP= BCP=  BPC=(180o-48o)/2=66o.
La respuesta es (d). BPC=(180o-48o)/2=66o.
La respuesta es (d).
Regresar al problema
Solución 73.
Como -1 es solución de la ecuación, entonces 3-b+c=0,
de ahí b-c=3, por lo cual uno de ellos (b o c)
tiene que ser impar, y el otro debe ser 2 (b y c son primos
y su diferencia es impar). Como b=c+3 y ambos son positivos, necesariamente
c=2
y b=5. Por lo tanto 3c - b =3 x 2 - 5 = 1. La respuesta es
(b).
Regresar al problema
Solución 74.
Cada término de la sucesión después del primero
(2, que es primo) es de la forma n2-1=(n+1)(n-1) con
n
entero positivo. La única manera de que un número de la sucesión
sea primo es que n-1=1, lo que implica que
n=2. En este caso,
n2-1=3,
el segundo número de la sucesión. Por lo tanto el 2 y el
3 son los únicos primos que aparecen. La respuesta es (b).
Regresar al problema
Solución 75.
Llamemos A, B, C y D a los vértices
como se indica en la figura. Un triángulo con vértices sobre
los puntos de la figura debe tener forzosamente 1 o 2 vértices sobre
los puntos del segmento AC. Hay 10 parejas distintas de puntos sobre
AC
que pueden ser vértices de un triángulo junto con otro punto
de los dos que hay sobre el segmento BC (sin contar el punto B),
por lo tanto hay 10 x 2=20 triángulos de este tipo. Si sólo
hay un punto sobre AC, quiere decir que es alguno de los 4 puntos
sobre AC que son distintos a B. Los otros dos vértices
en el segmento BD que son distintos a B son la pareja de
vértices que hace falta para completar un triángulo, por
lo cual sólo hay 4 triángulos de este tipo. En total hay
20 + 4 = 24 triángulos sobre los puntos de la figura. La respuesta
es (b).
Regresar al problema
Inicio de la página
|








 <2, así que la moneda toca a lo
más 3 cuadros horizontales y 3 verticales. Entonces el problema
se reduce a considerar una cuadrícula de 3 x 3. Si la moneda cubre
un pedazo de algún cuadro de la esquina, entonces no cubre el de
la esquina contraria porque la mínima distancia entre las dos esquinas
opuestas es
<2, así que la moneda toca a lo
más 3 cuadros horizontales y 3 verticales. Entonces el problema
se reduce a considerar una cuadrícula de 3 x 3. Si la moneda cubre
un pedazo de algún cuadro de la esquina, entonces no cubre el de
la esquina contraria porque la mínima distancia entre las dos esquinas
opuestas es  (la diagonal del cuadrado). Son 4 esquinas, entonces
hasta ahora hemos visto que a lo más la moneda cubre 7 cuadritos.
Ahora veamos que sí es posible lograr cubrir 7 cuadritos. Para esto
observemos que si colocamos la moneda circunscribiendo el cuadro central,
entonces cubrirá (parcialmente) 5 cuadros; la recorremos hacia arriba
un poco (menos de
(la diagonal del cuadrado). Son 4 esquinas, entonces
hasta ahora hemos visto que a lo más la moneda cubre 7 cuadritos.
Ahora veamos que sí es posible lograr cubrir 7 cuadritos. Para esto
observemos que si colocamos la moneda circunscribiendo el cuadro central,
entonces cubrirá (parcialmente) 5 cuadros; la recorremos hacia arriba
un poco (menos de  /2)para lograr que cubra todos los cuadros
salvo las esquinas inferiores. La respuesta es (d).
/2)para lograr que cubra todos los cuadros
salvo las esquinas inferiores. La respuesta es (d).


