|
|
Solución 26.
Trazando las diagonales del rectángulo encontramos 12 triángulos.
Cada lado del rectángulo contiene la base de 3 triángulos,
uno blanco y uno gris, de la misma área, pues sus bases y sus alturas
son iguales. Así, la razón de las áreas es de 1 a
2. La respuesta es (b).
Regresar al problema
Solución 27.
El número 1092 se escribe como un 1 seguido de 92
ceros. Entonces 1092-92 se escribe como noventa 9's seguidos
de un 0 y un 8. Tenemos que 9 x 90 + 0 + 8 = 818. La respuesta es (c).
Regresar al problema
Solución 28.
Escribí 5 cien veces como cifra de las unidades: 5, 15, 25,
..., 95, ..., 995. Escribí 5 cien veces como cifra de las decenas:
50, ...,59, 150, ..., 159, ..., 950, ..., 959. Escribí 5 cien veces
como cifra de las centenas: 500, 501, ..., 599. En total escribí
300 veces la cifra 5. La respuesta es (e).
Regresar al problema
Solución 29.
Por ser el número múltiplo de 5, debe terminar en 0 o
5, pero como no debe tener 0's, el número termina en 5. Ahora
hay que buscar tres números cuya suma sea 4 (pues la suma de todas
las cifras del número es 9); como ninguno debe ser cero la única
posibilidad es que sean 1,1,2 y, como el número debe ser mayor que
1995, debe ser 2115. Por lo tanto su tercera cifra es 1. La respuesta es
(a).
Regresar al problema
Solución 30.
El segmento MS es la diagonal de un rectángulo, por lo
cual los 2 triángulos que lo tienen como lado son de la misma área.
Lo mismo pasa con MQ y con QS, lo cual implica que las áreas
de los rectángulos grises siempre son iguales. La respuesta es (c).
Regresar al problema
Solución 31.
Por ser el número múltiplo de 5, debe terminar en 0 o
5, pero como no debe tener 0's, el número termina en 5. Ahora
hay que buscar tres números cuya suma sea 4 (pues la suma de todas
las cifras del número es 9); como ninguno debe ser cero la única
posibilidad es que sean 1,1,2 y, como el número debe ser mayor que
1995, debe ser 2115. Por lo tanto su tercera cifra es 1. La respuesta es
(a).
Regresar al problema
Solución 32.
Hay 6 formas de ir de la ciudad A a la ciudad D pasando
por B, y hay 10 formas pasando por C. Por lo tanto hay 16
rutas de la ciudad A a D. La respuesta es (b).
Regresar al problema
Solución 33.
Tenemos tres direcciones que pueden seguir las líneas de alambre,
las cuales podríamos pensar como: de izquierda a derecha, de adelante
a atrás y de arriba a abajo. En cada una de estas direcciones hay
16 líneas de 3 cm cada una pues son 4 niveles y en cada nivel hay
4 líneas. De esta manera tenemos que el resultado es 3 x 3 x 16
= 144. La respuesta es (e).
Regresar al problema
Solución 34.
Llamemos a y b a los catetos del triángulo y c
a su hipotenusa. Sabemos que c = 6 y que a+b+c=14.
Por lo tanto a+b=8. Elevando al cuadrado tenemos que (a+b)2=82,
lo cual implica que a2+2ab+b2=64.
El área que buscamos es ab/2. Por el Teorema de Pitágoras
c2+2ab=64,
sustituyendo c obtenemos que
ab/2=7, que es el área
que buscábamos. La respuesta es (b).
Regresar al problema
Solución 35.
La cantidad de días que pasan antes de que vuelvan a reunirse
todos debe ser divisible por 1, 2, 3, 4, 5, 6 y 7. Si multiplicamos 4 x
3 x 5 x 7=420 tenemos el mínimo común múltiplo los
números, así, el menor número de días en el
que se reencontrarán es 420. La respuesta es (d).
Regresar al problema
Solución 36.
El área del círculo es  x ( x ( /2)2= /2)2= /2.
El área de la superficie delimitada por los segmentos AD,
DC
y el arco AC es 1 - /2.
El área de la superficie delimitada por los segmentos AD,
DC
y el arco AC es 1 -  /4. El área de la región
delimitada por el segmento BC y el arco BC es la cuarta parte
de restarle al área del círculo el área del cuadrado,
o sea ( /4. El área de la región
delimitada por el segmento BC y el arco BC es la cuarta parte
de restarle al área del círculo el área del cuadrado,
o sea ( /2 - 1)/4 =1 - /2 - 1)/4 =1 -  /8 - 1/4}. Así, el
área de la región sombreada es 2( /8 - 1/4}. Así, el
área de la región sombreada es 2( /8 - 1/4 + 1 - /8 - 1/4 + 1 -  /4)=1/2.
La respuesta es (c). /4)=1/2.
La respuesta es (c).
Regresar al problema
Solución 37.
Uno de los enteros, digamos a, debe ser par, mientras que el
otro, b, debe ser impar. Como 43 = 64 > 57, tenemos que
a
= 2; entonces es fácil ver que b=5. La respuesta es (b).
Regresar al problema
Solución 38.
El triángulo ABC es isósceles (AB = AC),
lo que implica que  ABC = ABC =  ACB = 75o,
y que ACB = 75o,
y que  BAC = 180o-(75o+75o)
= 30o. El triángulo ADC es isósceles (AD=DC),
lo que implica que BAC = 180o-(75o+75o)
= 30o. El triángulo ADC es isósceles (AD=DC),
lo que implica que  DAC = DAC =  DCA = (180o-50o)/2
= 65o. Observemos que DCA = (180o-50o)/2
= 65o. Observemos que  BAD = BAD =  CAB
+ CAB
+  DAC = 30o+65o=95o. La respuesta es (d). DAC = 30o+65o=95o. La respuesta es (d).
Regresar al problema
Solución 39.
En la figura, el área del triángulo ABC es igual
a la del triángulo FGH, y el área del triángulo
ACD
es igual a la del EIJ. Así, el área sombreada es igual
al área del cuadrado EFHI, que es 9. Entonces la respuesta
es (a).
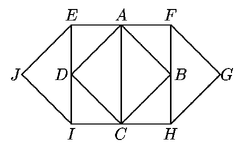
Regresar al problema
Solución 40.
Si el promedio de los cinco números es 40, entonces su suma
es 40 x 5=200. De la misma manera, la suma de los tres que no se eliminaron
es 108. Entonces, los dos eliminados suman 92 y su promedio es 46. La respuesta
es (d).
Regresar al problema
Solución 41.
Tenemos que CANGUROS = 10,000 x CANG +
UROS,
así es que
10,000 x UROS- 10,000 x CANG+ 10,000 x CANG+
UROS=10,000
x UROS+ UROS= UROSUROS.
La respuesta es (a).
Regresar al problema
Solución 42.
El ángulo A'BC mide 180o - 2(72o)=36o.
Por lo tanto, la región sombreada es 360o/36o=1/10
del área total del círculo con centro en B y radio
AB,
que es  (12)=/pi. El área de la región sombreada es
igual a (12)=/pi. El área de la región sombreada es
igual a  /10}. La respuesta es (c). /10}. La respuesta es (c).
Regresar al problema
Solución 43.
Queremos que el número sea múltiplo de 6, por tanto debe
serlo de 2 y de 3. Al pedir que la suma de sus cifras sea 21 el número
ya será múltiplo de 3. El número deberá además
par, así es que pensemos en las posibilidades para su última
cifra. El número no puede terminar en 0 ni 2 porque no tenemos posibilidades
para las primeras dos cifras de forma que la suma alcance 21. Si la última
cifra es 4, las dos primeras deben sumar 17, así es que deben ser
8 y 9, y hay dos combinaciones posibles: 984 y 894. Si la última
cifra es 6, las primeras pueden ser 8 y 7, o bien 9 y 6, con los que se
pueden formar cuatro números: 876, 786, 966 y 696. Si la última
cifra es 8, las posibilidades para las primeras son 6 y 7, 5 y 8, o bien
4 y 9; y hay 6 números: 768, 678, 588, 858, 498, 948. En total hay
12 números. La respuesta es (c).
Regresar al problema
Solución 44.
x2/2 es par siempre. Como x es par, entonces
x
es múltiplo de 2 y, por lo tanto, x2 es múltiplo
de 4. Entonces x2/2 es múltiplo de 2, es decir,
es par. La respuesta es (c) .
Regresar al problema
Solución 45.
Observemos que 343=73. Como los números son de cuatro
cifras, 3 de ellas son 7 y la otra es 1. Entonces las únicas posibilidades
son 7177, 7717, 7771. La respuesta es (c).
Regresar al problema
Solución 46.
El área del círculo es  (12)= (12)= , así que
estamos buscando la altura de un triángulo equilátero que
tiene área , así que
estamos buscando la altura de un triángulo equilátero que
tiene área  . AB'C' es un triángulo equilátero,
aplicando el Teorema de Pitágoras al triángulo rectángulo
que tiene como hipotenusa a AC' y como catetos a la altura trazada
desde el vértice A y a la mitad del lado B'C'. Si
AC'
mide b y la altura es h, tenemos que h2=b2-(b/2)2=(3/4)b2,
de donde b=(2/ . AB'C' es un triángulo equilátero,
aplicando el Teorema de Pitágoras al triángulo rectángulo
que tiene como hipotenusa a AC' y como catetos a la altura trazada
desde el vértice A y a la mitad del lado B'C'. Si
AC'
mide b y la altura es h, tenemos que h2=b2-(b/2)2=(3/4)b2,
de donde b=(2/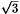 )h. El área del triángulo
es hb/2. Así, (1/ )h. El área del triángulo
es hb/2. Así, (1/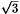 )h2= )h2= y h= y h=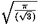 .
La respuesta es (a). .
La respuesta es (a).
Regresar al problema
Solución 47.
Aplicando el Teorema de Pitágoras al triángulo cuya hipotenusa
es el radio de la esfera y uno de cuyos lados es el radio del agujero,
vemos que la distancia desde el centro de la esfera hasta el nivel de la
mesa es 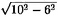 =8. Así, la distancia
del punto más alto de la esfera al piso es 10+8+30=48. La respuesta
es (d). =8. Así, la distancia
del punto más alto de la esfera al piso es 10+8+30=48. La respuesta
es (d).
Regresar al problema
Solución 48.
Si la fecha menor del cuadrado es x, la suma de todas las fechas
del cuadrado es
x + x + 1 + x + 2 + x + 7 + x + 8
+ x + 9 + x + 14 + x + 15 + x + 16 = 9x
+
72 = 9x + 7x(10) + 2.
Necesitamos que 9x termine en 8, lo cual es posible si x
termina en 2. Para que x sea múltiplo de 4 la única
posibilidad es x=12. Entonces, la fecha de la esquina inferior derecha
es 28. La respuesta es (e).
Regresar al problema
Solución 49.
Como sabemos cuánto vale f(2), podríamos
calcular f(11) si conociéramos el valor de f(3)
ya que 11 = 4+4+3 = (2+2)+(2+2)+3. Tenemos que f(4) = f(2+2)
=
f(2)
+
f(2)
+
4 = 10. Por otra parte
f(4)
= 10 = f(3)
+ f(1)
+
3, de donde
f(3)
= 7-f(1). Además
f(3)=f(2+1)=f(2)+f(1)+2=f(1)+5.
Tenemos dos ecuaciones que involucran a f(3) y a f(1).
Resolviendo obtenemos f(1)=1 y f(3)=6. Entonces
f(11)
=
f(4+7)
=
f(4)
+
f(4+3)
+
28 = 10 + f(4)
+
f(3)
+ 12 + 28 = 50 + 10 +
6 = 66. La respuesta es (e).
Regresar al problema
Solución 50.
En (1+12)+(2+22)+(3+32)+ ... +(2001+20012)
podemos reemplazar cada número por su última cifra sin alterar
la última cifra del resultado. Asi, la última cifra de la
suma es la misma que la última cifra de 200 x ((1+12)
+ (2+22) + (3+32) + ... + (10+102)) +
(1+12) = 88002. Por lo tanto, la cifra que buscábamos
es 2. La respuesta es (b).
Regresar al problema
Inicio de la página
|








