|
|
Décima Segunda Olimpiada Nacional de
Matemáticas
Querétaro, Querétaro, noviembre de 1998
Primer Día
Problema 1.
Un número es suertudo si al sumar los cuadrados de sus cifras y
repetir esta operación suficientes veces obtenemos el número
1. Por ejemplo, 1900 es suertudo, ya que 1900 
82
68 100 1. Encuentre una infinidad de parejas de enteros
consecutivos, donde ambos números sean suertudos.
Problema 2.
Dos rayos l y m parten de un mismo punto formando un
ángulo 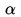 , sea P un punto en l.
Para cada
circunferencia  tangente a en P que
corte
a m en puntos Q y R, sea T el punto donde la
bisectriz del
ángulo QPR corta a C. Describa la figura
geométrica que
forman los puntos T. Justifique su respuesta.
Problema 3.
Cada uno de los lados y las diagonales de un octágono regular se
pintande de rojo o negro. Demuestre que hay al menos siete
triángulos cuyos vértices son vértices del
octágono y sus tres lados son del mismo color.
Segundo Día
Problema 4.
Encuentre todos los enteros que se escriben como
1/a1+2/a2+...9/a9,
donde a1, a2, ..., a9 son
dígitos distintos de cero que pueden repetirse.
Problema 5.
Sean B y C dos puntos de una circunferencia, AB y
AC
las tangentes desde
A. Sea Q un punto del segmento AC y P la
intersección de BQ con la
circunferencia. La paralela a AB por Q corta a BC en
J. Demuestre que PJ
es paralelo a AB si y sólo si BC2= AC x
CQ.
Problema 6.
Un plano en el espacio es equidistante a un conjunto de puntos si la
distancia de cada punto al plano es la misma. ¿Cuál es el
mayor
número de planos equidistantes a 5 puntos de los cuales no hay 4 en
un mismo plano?
|
