|
|
Décima Segunda Olimpiada Nacional de
Matemáticas
Querétaro, Querétaro, noviembre de 1998
Soluciones
Problema 1
Claramente 10 es suertudo, y como
12 + 32 = 32 + 12 = 10,
tenemos que 13
y 31 también lo son. Sucede que
32 + 22 = 13, por
lo que 32 es suertudo. Entonces, 31 y 32 son dos
suertudos consecutivos y por lo tanto para cualquier N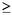 1, 1,
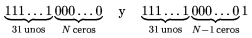
son dos enteros suertudos consecutivos.
Alternativamente, si n y n + 1 son ambos suertudos,
también lo son
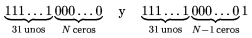
Y repitiendo la construcción, hallamos una infinidad de parejas
de
enteros suertudos consecutivos.
Problema 2
Sea A el punto de donde parten los rayos, 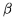 el ángulo QPT que es igual al ángulo TPR y
el ángulo QPT que es igual al ángulo TPR y
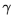 el ángulo QRP que es igual al
ángulo QPA. El ángulo QPR es un ángulo
externo al triángulo APQ, y es igual a el ángulo QRP que es igual al
ángulo QPA. El ángulo QPR es un ángulo
externo al triángulo APQ, y es igual a 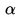 + +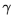 . Considerando
el triángulo PQR, . Considerando
el triángulo PQR, 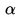 +2 +2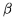 +2 +2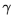 = =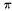 , de donde , de donde
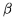 + + =1/2( =1/2( - - ), a partir de la
intersección
de este rayo con m. ), a partir de la
intersección
de este rayo con m.
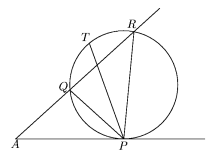
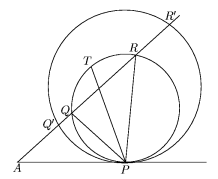
Solución alternativa para ver la medida del ángulo
APT. Supongamos que una circunferencia 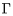 es
tangente a l en P y corta a m en Q y en
R y que otra circunferencua es
tangente a l en P y corta a m en Q y en
R y que otra circunferencua 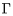 '
también es tangente a l en P y que corta a m
en Q' y en R' con los puntos sobre m en el orden
Q',Q,R,R'. Sea A el punto del que parten los rayos l
y m. Como l es tangente a '
también es tangente a l en P y que corta a m
en Q' y en R' con los puntos sobre m en el orden
Q',Q,R,R'. Sea A el punto del que parten los rayos l
y m. Como l es tangente a 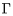 , ,
 QPA= QPA= QRP y
análogamente, QRP y
análogamente,  Q'PA=Q'RP. Entonces, Q'PA=Q'RP. Entonces,
 QPQ'= QPQ'= QPA- QPA- Q'PA= Q'PA= QRP- QRP- QR'P= QR'P= RPR'. RPR'.
Entonces, los ángulos QPR y Q'PR' tienen la misma
bisectriz y por lo tanto la bisectriz de QPR no depende de la
circunferencia 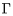 que se
trace. Podemos entonces
calcular el ángulo entre la bisectriz y el rayo tomando la
circunferencia que
es tangente a l en P y tangente a m en Q =
R. Como APQ es un triángulo isósceles, el
ángulo buscado es que se
trace. Podemos entonces
calcular el ángulo entre la bisectriz y el rayo tomando la
circunferencia que
es tangente a l en P y tangente a m en Q =
R. Como APQ es un triángulo isósceles, el
ángulo buscado es  APQ = 90o - APQ = 90o - /2 /2
Problema 3
Con triángulos nos referiremos a un triángulo con
vértices en el octágono, y con ángulo a dos lados de
un triángulo. Un ángulo es bicolor si sus lados son de color
distinto. Nos fijamos en un vértice del octágono, si k de
las líneas que lo unen con los otros vértices son de un
color (y 7-k del otro), entonces es vértice de
k(7-k)  3 x 4 ángulos bicolor. Luego el
número de á:ngulos bicolor es 3 x 4 ángulos bicolor. Luego el
número de á:ngulos bicolor es  b b  8 x 3 x 4 = 96. Cada triángulo bicolor
tiene
exactemente dos ángulos bicolor, así el número de
triángulos bicolor es 1/2 8 x 3 x 4 = 96. Cada triángulo bicolor
tiene
exactemente dos ángulos bicolor, así el número de
triángulos bicolor es 1/2 b y por lo tanto el número de
triángulos monocromáticos es b y por lo tanto el número de
triángulos monocromáticos es  m= m=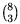 -1/2 -1/2 b b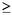 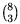 -96/2 = 8. Entonces
siempre
hay 8 triángulos monocromáticos (se pide probar que hay al
menos 7). -96/2 = 8. Entonces
siempre
hay 8 triángulos monocromáticos (se pide probar que hay al
menos 7).
Solución Alternativa. Probaremos primero que en un
hexágono se forman dos triángulos
monocromáticos. Desde luego hay uno: nos fijamos en un
vértice A cualquiera del hexágono, de él salen
cinco líneas de las cuales al menos tres son de un color,
supongamos que AB, AC y AD son rojas. Si una de
BC, CD o DB fuera roja, entonces uno de los
triángulos ABC, ACD o ABD sería un
triángulo rojo y si las tres son negras, BCD sería un
triángulo negro. De cualquier forma hay un triángulo
monocromático, sea V uno de sus vértice. Los otros
cinco vértices del hexágono forma un pentágono, si en
el pentágono hay un triángulo monocromático, en el
hexágono hay dos. Si en el pentágono no hay un
triángulo monocromático, de cada vértice deven salir
dos líneas de cada color y el pentágono se puede descomponer
en dos ciclos: uno rojo y uno negro. Al considerar el vértice V es
fácil ver que en este caso también hay dos triángulos
monocromáticos.
Ahora veremos que en un heptágono se forman cuatro
triángulos monocromáticos. Sean A, B,
C, D, E, F y G los véretices del
heptágono. En el hexágono BCDEFG sabemos que hay dos
triángulos monocromáticos, supongamos que B es uno de
los vértices de uno de esos triángulos. Como en el
hexágono ACDEFG hay dos triángulos
monocromáticos, en el heptágono hay tres: esos dos y el que
tiene a B como vértice. Algún vértice del
heptágono tiene que ser vértice de dos de esos
triángulos, supongamos que es G. En el hexágono
ABCDEF hay dos triángulos monocromáticos y por lo
tanto en el heptágono hay cuatro: esos dos y los dos de
vértice G.
Finalmente, mostraremos que en un octágono se forman siete
triángulos monocromáticos. Sea ABCDEFGH el
octágono. En el heptágono BCDEFGH hay cuatro
triángulos monocromáticos, dos de ellos comparten un
vértice, digamos B. Ahora, en el heptágono
ACDEFGH, hay cuatro triángulos monocromáticos
distintos de los otros dos. Un vértice del octágono debe
estar en tres de los seis triángulos monocromátiucos y con
los tres que tienen a H como vértice tenemos siete
triángulos monocromáticos.
Problema 4
Los enteros de esa forma son los del 5 al 45. Con
a1=a2=...=a9=1
obtenemos el mayor de esos números, 45. Con
a1=a2=...=a9=9
obtenemos el menor, 5. Como
1/7
+
2/7
+ ... + 7/7 = 28/7 = 4,
se pueden escribir 6, 7, 8 y 9 así:
1/7
+
2/7
+
... +
7/7
+ 8/8 + 9/9 = 6
1/7
+
2/7
+
... +
7/7
+ 8/4 + 9/9 = 7
1/7
+
2/7
+
... +
7/7
+ 8/8 + 9/3 = 8
1/7
+
2/7
+
... +
7/7
+ 8/2 + 9/9 = 9
Si tomamos cada ai=i, cada fracción es igual a
1 y obtenemos 9 sumándolas. Si cambiamos alguna
ai de i a 1, la suma aumenta
i/1-i/i=i-1, entonces
podemos conseguir aumentos
(independientes) de 1,2,3,...8 y así formamos los
números del 10 al 45.
Problema 5
Como JQ es paralela a AB,  JQP= JQP= QBA y QBA y  QBA= QBA= JCP
por que subtienden el mismo arco en la circunferencia. Por lo tanto,
JPQC es un cuadrilátero cíclico. JCP
por que subtienden el mismo arco en la circunferencia. Por lo tanto,
JPQC es un cuadrilátero cíclico.
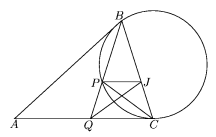
Por otro lado:
BC2=AC QC

BC/AC=QC/BC

 BCA BCA  QCB (porque comparten el ángulo C) QCB (porque comparten el ángulo C)

 PQC= PQC= JCQ (porque JCQ (porque  BCA es isósceles) BCA es isósceles)

JPQC es un trapecio isósceles (porque JPQC es
cíclico)

JP es paralelo a QC (otra vez porque JPQC es
cíclico),
donde usamos dos veces que los únicos
trapecios
cíclicos son los isósceles.
Problema 6
Para cada plano equidistante P, los cinco puntos A,
B, C, D, E están en dos planos
paralelos a P, dos en uno y tres en el otro. Recuerde que no hay
cuatro puntos en un mismo plano.
Tomemos cuatro de los puntos, digamos A, B, C y
D, y veamos donde puede colocarse el quinto punto E para
obtener la mayor cantidad de planos equidistantes. Si los cinco puntos se
deben dividir en dos conjuntos, uno de dos elementos y otro de tres,
tenemos que hay dos posibilidades: (1) que E esté en un
conjunto de tres elementos, y (2) que E esté en un conjunto
de dos elementos.
En el caso (1) formemos primero un paralelepipedo de caras paralelas
a– lplano que determinan aristas opuestas del tetraedro ABDCE deberá unirse a un par de puntos del conjunto {A,
B, C, D} y entonces determinará un plano que
será paralelo tanto al otro plano que pasa por los otros dos puntos
como al plano equidistante correspondiente, esto se puede hacer de
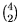 = 6 maneras y los planos que se determinan
así son los planos que conteinen a las caras del
paralelepípedo, siendo la cara paralela la otra donde se encuentran
los otros dos puntos y determinando como plano equidistante el plano
paralelo a los anteriores que pasa por los puntos medios de las cuatro
aristas que no están sobre los dos primeros planos, así en
éste caso solamente hay tres posibles planos equidistantes y
éstos se logran cuando el punto E es cualquier
vértice del paralelepípedo diferente de A, B,
C, D. = 6 maneras y los planos que se determinan
así son los planos que conteinen a las caras del
paralelepípedo, siendo la cara paralela la otra donde se encuentran
los otros dos puntos y determinando como plano equidistante el plano
paralelo a los anteriores que pasa por los puntos medios de las cuatro
aristas que no están sobre los dos primeros planos, así en
éste caso solamente hay tres posibles planos equidistantes y
éstos se logran cuando el punto E es cualquier
vértice del paralelepípedo diferente de A, B,
C, D.
En el caso (2) E deberá unirse a uno de los puntos A,
B, C, D y los restantes 3 estarán en un plano
paralelo al equidistante, esto se puede hacer de cuatro maneras y los
planos donde E puede estar son los planos paralelos a las carasdel
tetraedro ABCD que pasan por el vértice que no
está en la cada que se está considerando; estos planos
forman otro tetraedro semejante al ABCD. Claramente E no puede
estar en los cuatro planos, pero si en tres, cuando E es uno de los
vértices de este nuevo tetraedro, en cuyo caso se obtienen
también tres planos equidistantes.
|







