|
|
Décima Olimpiada Nacional de Matemáticas
Mérida, Yucatán, noviembre de 1996
Primer Día
Problema 1.
Sea ABCD un cuadrilátero y sean P y Q los
puntos de trisección de la diagonal BD (es decir, P y
Q son los puntos del segmento BD para los cuales las
longitudes BP, PQ y QD son todas iguales).
Sea E la intersección de la recta que pasa por A y
P con el segmento BC y sea F la intersección
de la recta que pasa por A y Q con el segmento DC.
Demuestra lo siguiente:
(i) Si ABCD es paralelogramo, entonces E y F son los
respectivos puntos medios de los segmentos BC y CD.
(ii) Si E y F son los puntos medios de BC y
CD, respectivamente, entonces ABCD es un paralelogramo.
Problema 2.
Bordeando una mesa circular hay dibujadas 64 casillas y en cada una hay
una ficha. Las fichas y las casillas están numeradas del 1 al 64 en
orden sucesivo (cada ficha está en la casilla que lleva el mismo
número). En la parte central de la mesa hay 1996 focos apagados.
Cada minuto todas las fichas se desplazan simultáneamente, en forma
circular (en el el mismo sentido de la numeración), como sigue: la
ficha #1 se desplaza una casilla, la ficha #2 se desplaza
dos casillas, la ficha #3 se desplaza tres casillas,
etcétera, pudiedo varias fichas ocupar la misma posición.
Cada vez que una ficha comparte el lugar en una casilla con la ficha
#1, se prende uno de los focos (se prenden tantos focos como fichas
estén compartiendo la posición con la ficha #1 en ese
momento). ¿En dónde estará la ficha #1 en el
primer momento en que ya todos los focos estén prendidos?
Problema 3.
Demuestra que no es posible cubrir una cuadrícula de 6 x 6
con 18 rectángulos de 2 x 1, de tal manera que cada una de
las rectas de longitud 6 que forman la cuadrícula y que
están en el interior de la misma pase por el centro de por lo menos
uno de los rectángulos. Demuestra también que sí es
posible cubrir una cuadrícula de 6 x 5 con 15
rectángulos de 2 x 1, de tal manera que cada una de las
rectas de longitudes 5 o 6 que forman la cuadrícula y que
están en el interior de la misma pase por el centro de por lo menos
uno de los rectángulos.
Segundo Día
Problema 4.
¿Para qué enteros n 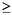 2 se
pueden acomodar los números del 1 al 16 en los cuadros de una
cuadrícula de 4 x 4 (un número en cada cuadro, sin
repetir números) de tal manera que las 8 sumas de los
números que quedan en cada fila y en cada columna sean
múltiplos de n, y que estos 8 múltiplos sean todos
distintos entre sí?
Problema 5.
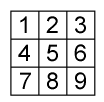
En una cuadrícula de n x n se escriben los números
del 1 al n2 en el orden habitual (de izquierda a derecha
y de arriba a abajo, como se ilustra en la figura para el caso
n=3).
Llamamos camino en la cuadrícula a una sucesión de
pasos de un cuadro a otro, desde el cuadro que tiene el número 1
hasta el que tiene el número n2, de tal manera
que en cada paso el movimiento sea hacia la derecha o hacia abajo. Si  es un camino, denotamos por L() a la suma de los números por los que pasa el
camino .
(i) Sea M la mayor L() que se puede
obtener de entre todos los caminos en una
cuadrícula fija de tamaño n x n y sea m la
menor L() (también de entre todos los
caminos en una cuadrícula fija de
tamaño n x n). Prueba que M-m es un cubo perfecto.
(ii) Prueba que en ninguna cuadrícula hay un camino tal que L()= 1996.
Problema 6.
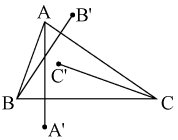
En la figura se muestra un triángulo acutángulo ABC
en el que la longitud de AB es menor que la de BC y la
longitud de BC es menor que la de AC. Los puntos A',
B', y C' son tales que AA' es perpendicular a
BC y la longitud de AA' es igual a la de BC;
BB' es perpendicular a AC y la longitud de BB' es
igual a la de AC; CC' es perpendicular a AB y la
longitud de CC' es igual a la de AB. Además el
ángulo  AC'B es de 90o.
Demuestra que A', B' y C' están alineados.
|
