|
 |
 |
|
 |
|||
|
|
Mérida, Yucatán, noviembre de 1996 |
| Posición de la Ficha #1 | 2 | 4 | 6 | 8 | 10 | 12 | 14 | 16 | 18 | 20 | 22 | 24 | 26 | 28 | 30 | 32 |
| Coincidencias | 1 | 3 | 1 | 7 | 1 | 3 | 1 | 15 | 1 | 3 | 1 | 7 | 1 | 3 | 1 | 31 |
Hasta aquí se juntan 80, así que la ficha #1
estará en la casilla 32 cuando todos los focos queden prendidos.
(Para ver las coincidencias por columnas formalmente, consideremos lo
siguiente: Cuando la ficha #1 está en el lugar
2ab, con b impar, el número de
coincidencias es el número de elementos del conjunto {x | 1 < x
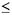 64, 2abx
64, 2abx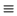 2ab (mod 26-a)}. Como la
congruencia es equivalente a x
2ab (mod 26-a)}. Como la
congruencia es equivalente a x 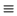 1 (mod
26-a), el número de coincidencias en esa casilla es
de 2a-1.)
1 (mod
26-a), el número de coincidencias en esa casilla es
de 2a-1.)
Problema 3
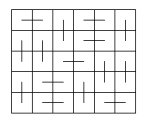
Supongamos que sí es posible cubrir la cuadrícula de 6 x 6 con la propiedad mencionada. Primero observemos que, en este caso, cada línea interior vertical deberá estar atravesada por un número par de rectangulitos horizontales; para ver esto observemos que cada rectangulito vertical abarca dos cuadritos verticales y 6 es un número par, de tal suerte que entonces en la primera columna vertical habrá un numero par de rectángulos horizontales; pero entonces, en la segunda columna pasará lo mismo puesto que los rectángulos horizontales que cubren cuadritos en la primera columna abarcan un número par en esta segunda, así que los cuadritos que quedan en esta columna también son un número par, y así sucesivamente. Por la condición pedida en el problema, cada línea interior vertical estará atravesada entonces por al menos dos rectangulitos horizontales. Por la misma razón, cada línea interior horizontal estará atravesada por dos rectangulitos verticales. Sin embargo, el número total de líneas interiores es 10 (5 verticales y 5 horizontales) y cada uno de los 18 rectangulitos sólo puede atravesar una de ellas, así que no puede haber las 20 intersecciones que se dice arriba que debe haber. Entonces no es posible cubrir la cuadrícula como se estaba suponiendo.
Una forma para cubrir la cuadrícula de 6 x 5 con
la condición pedida se muestra en la siguiente figura.
Supongamos que para cierta n 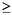 2
sí es posible llenar la cuadrícula como se pide y veamos
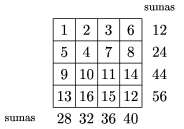
cómo debe ser n. La mínima suma posible por
renglones o columnas es 10(=1+2+3+4) y la máxima suma
posible es 58(=13+14+15+16). Se necesitan 8 múltiplos
distintos de n pues hay 4 filas y 4 columnas, pero
58-10/8=6, así que n
2
sí es posible llenar la cuadrícula como se pide y veamos
cómo debe ser n. La mínima suma posible por
renglones o columnas es 10(=1+2+3+4) y la máxima suma
posible es 58(=13+14+15+16). Se necesitan 8 múltiplos
distintos de n pues hay 4 filas y 4 columnas, pero
58-10/8=6, así que n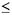 6 (por ejemplo, entre 10 y 58 no podemos
encontrar 8 múltiplos distintos de 7 ya que entre 10 y 58
sólo hay 7 múltiplos de 7 que son: 14, 21, 28, 34, 42,
49 y 56).
6 (por ejemplo, entre 10 y 58 no podemos
encontrar 8 múltiplos distintos de 7 ya que entre 10 y 58
sólo hay 7 múltiplos de 7 que son: 14, 21, 28, 34, 42,
49 y 56).
Ahora observemos que la suma de todos los
números del 1 al 16 es 136, así que este número
también se obtiene sumando los 4 múltiplos de n
que aparezcan por filas, de donde n no puede ser 3, 5 o 6 pues
estos no son divisores de 136. Para ver que los casos n=2 y
n=4 sí son posibles, consideremos, por ejemplo, los
acomodos de las figuras, en donde el caso n=4 se obtuvo del caso
n=2 intercambiando las posiciones de 4 y 6 y las de 12, 16 y 14
(estos últimos tres en forma cíclica).
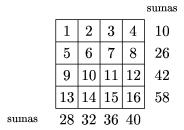
Observemos primero que cada camino  cruza exactamente una vez cada una de las diagonales que se muestran
en la figura.
cruza exactamente una vez cada una de las diagonales que se muestran
en la figura.
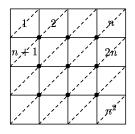
El mínimo valor de un número en cada diagonal está arriba a la derecha y el máximo está abajo a la izquierda, así que m se logra con el camino que va todo a la derecha hasta terminar el primer renglón y después hacia abajo por la última columna, y M se logra con el camino que primero va hacia abajo recorriendo toda la primera columna y después hacia la derecha por el último renglón. Así
Además observemos que sobre las diagonales en cuadritos juntos, la diferencia es de n-1.
Entonces M-m=(n-1)2(n-1)=(n-1)3 (pues
en cada  en la cuadrícula hay una diferencia
de
n-1 y hay (n-1)2
en la cuadrícula hay una diferencia
de
n-1 y hay (n-1)2  's.
's.
Ahora, si buscamos una n y un
camino  en una cuadrícula de n x
n que cumpla L(
en una cuadrícula de n x
n que cumpla L( )=1996, debemos tener
m
)=1996, debemos tener
m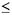 1996
1996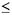 M. Pero
m= [1+2+...+(n-1)]+ [n+2n+3n+...+n2]=n(n-1)/
2+n x (
(n(n-1))/2)+n2=(n-1)n(n+1)
/2+n2, y M=m+(n-1)3, como
vimos arriba; entonces de m
M. Pero
m= [1+2+...+(n-1)]+ [n+2n+3n+...+n2]=n(n-1)/
2+n x (
(n(n-1))/2)+n2=(n-1)n(n+1)
/2+n2, y M=m+(n-1)3, como
vimos arriba; entonces de m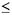 1996
obtenemos n
1996
obtenemos n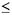 15 y de M
15 y de M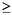 1996 obtenemos n
1996 obtenemos n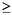 12 (pues
12 (pues
para n=15 tenemos m = (16 x15 x 14)/2 + 152 = 1905 < 1996,
para n=16 tenemos m = (17x16x15)/2 + 162 = 2296 > 1996,
para n=11 tenemos
M = (12x11x10)/2 + 112 +
103
= 1781 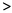 1996 y
1996 y
para n=12 tenemos M = (13x12x11)/2 + 122 + 113 = 2333 > 1996) .
Entonces los posibles valores para n son 12, 13, 14 y 15. Ahora recordemos que cualquier camino tiene diferencia un múltiplo de n-1 con el mínimo, así que debemos tener que 1996-m debe ser múltiplo de n-1. Calculemos entonces en cada caso 1996-m:
Si n=12, entonces m=1002 y 1996-m=994 que no es múltiplo de 11.
Si n=13, entonces m=1261 y 1996-m=735 que no es múltiplo de 12.
Si n=14, entonces m=1561 y 1996-m=435 que no es múltiplo de 13.
Si n=15, entonces m=1905 y 1996-m=91 que no es múltiplo de 14.
De los
cálculos anteriores concluimos que no es posible encontrar un
camino  con L(
con L( )=1996.
)=1996.
Problema 6
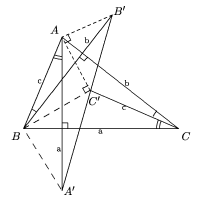
Observemos primero que  ABB'
=
ABB'
= C'CA puesto que ambos son complementarios
de
C'CA puesto que ambos son complementarios
de  BAC (ya que CC' es
perpendicular a AB y BB' es perpendicular a
AC). Entonces los triángulos ABB' y
C'CA son iguales (por tener iguales dos lados y el
ángulo comprendido entre ellos). Como dos lados
correspondientes en estos triángulos son perpendiculares entre
sí, entonces también lo es el tercero, es decir,
BAC (ya que CC' es
perpendicular a AB y BB' es perpendicular a
AC). Entonces los triángulos ABB' y
C'CA son iguales (por tener iguales dos lados y el
ángulo comprendido entre ellos). Como dos lados
correspondientes en estos triángulos son perpendiculares entre
sí, entonces también lo es el tercero, es decir,
 B'AC'= 90o. Por la
misma razón, los triángulos BCC' y
A'AB son iguales y
B'AC'= 90o. Por la
misma razón, los triángulos BCC' y
A'AB son iguales y  C'BA' =90o. Pero entonces
A'BC' y C'AB' son
triángulos rectángulos isósceles
(A'B=BC' y C'A=AB'), de
donde sus ángulos no rectos son de
45o. Así
C'BA' =90o. Pero entonces
A'BC' y C'AB' son
triángulos rectángulos isósceles
(A'B=BC' y C'A=AB'), de
donde sus ángulos no rectos son de
45o. Así
 A'C'B'=
A'C'B'= A'C'B +
A'C'B + BC'A +
BC'A + AC'B'= 45o+ 90o+ 45o=180o,
de donde A', C' y B' están alineados.
AC'B'= 45o+ 90o+ 45o=180o,
de donde A', C' y B' están alineados.