|
|
Novena Olimpiada Nacional de Matemáticas
Colima, Colima, noviembre de 1995
Primer Día
Problema 1.
En una Olimpiada de Matemáticas los concursantes
están
ocupando todos los asientos de un salón rectangular donde los
asientos
están alineados en filas y columnas de tal manera que hay
más de dos filas y en cada fila hay más de dos asientos. Al
inicio del examen un profesor les sugiere que se deseen suerte
dándose la mano; cada uno de los concursantes estrecha la mano de
los concursantes que están junto a él (adelante,
atrás, a los lados y en diagonal) y sólo a éstos.
Alguien observa que se dieron 1020 apretones de manos.
¿Cuántos concursantes hay?
Problema 2.
Considera 6 puntos en el plano con la propiedad de que 8 de las distancias
entre ellos son iguales a 1. Muestra que al menos tres de los puntos
forman un triángulo equilátero de lado 1.
Problema 3.
Sean A, B, C y D vértices consecutivos
de un heptágono regular; sean AL y AM las tangentes
desde A a la circunferencia de
centro C y radio CB. Sea N la intersección de
AC y BD. Demuestra que los puntos L, M y
N son colineales.
Segundo Día
Problema 4.
(a) Encuentra un subconjunto B del conjunto
A={1,2,3,...,40} de manera que B tenga 26 elementos y que
ningún producto de dos elementos de B sea un cuadrado
perfecto.
(b) Demuestra que no se puede obtener un subconjunto de A de 27
elementos con la característica mencionada en (a).
Problema 5.
Sea ABCDE un pentágono (convexo) de manera que los
triángulos ABC, BCD, CDE, DEA, y
EAB
son todos de igual área. Demuestra que:
1/4área(ABCDE) < área(ABC) <
1/3área(ABCDE).
Problema 6.
Sobre los cuadrados de una cuadrícula de 4 x 4 se colocan
símbolos 0 y 1; estos símbolos se cambian uno por el otro al
aplicar alguna de las siguientes tres operaciones: La operación (a)
cambia de símbolos todos los elementos de un renglón. La
operación (b) cambia de símbolos todos los elementos de una
columna. La operación (c) cambia de símbolos todos los
elementos de una diagonal (las diagonales son las que se muestran con
líneas punteadas en la figura).
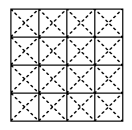
Determina cuáles son los arreglos de los que se puede partir
para que con un número finito de operaciones se pueda llegar a un
arreglo de puros símbolos 0.
|







