|
|
Novena Olimpiada Nacional de Matemáticas
Colima, Colima, noviembre de 1995
Soluciones
Problema 1
Sea n el número de filas y m la cantidad de
lugares en cada fila del salón.
(i) Cada una de las (n-2)(m-2) personas que están en el
interior del rectángulo saluda a 8 personas que están
a su alrededor.
(ii) Cada una de las 2[(n-2)+(m-2)] personas que están en
las orillas del rectángulo, pero no en las esquinas, saluda a
5 personas.
(iii) Las 4 personas de las esquinas saludan a 3.
Así contando los saludos dos veces y desarrollando tenemos que:
8(n-2)(m-2)+10[(n-2)+(m-2)]+12=2040
8nm-6n-6m=2036.
Para resolver esta ecuación podemos proceder de varias
maneras. Una de ellas podría ser buscando una factorización:
16mn-12m-12n = 4072
16mn-12m-12n+9 = 4081
4n(4m-3)-3(4m-3) = 4081
(4n-3)(4m-3)=4081 = 7x11x53
como 7 y 11 no son de la forma 4s-3, las
únicas soluciones son:
(4n-3=77 y 4m-3=53) o bien (4n-3=53 y 4m-3=77),
por lo que (n=20 y m=14) o bien (n=14 y m=20). En
cualquier caso el número de concursantes es de 280.
Otra forma para resolver la ecuación podría ser usando
congruencias: Tenemos que 4nm-3n-3m=1018, de donde
n(4m-3)=3m+1018. Simplificando módulo 4m-3 tenemos la
siguiente sucesión de congruencias equivalentes:
3m+1018 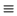 (mod 4m-3), (mod 4m-3),
12m+4072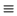 (mod 4m-3), (mod 4m-3),
3(4m-3)+4081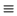 (mod 4m-3) y (mod 4m-3) y
4081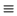 (mod 4m-3). (mod 4m-3).
Entonces 4m-3 es divisor de 4081 =7x11x53,
y así las posibilidades para 4m-3 son
1, 7, 11, 53, 77, 371, 583
y 4081. Como m y n no pueden ser 1, las únicas
posibilidades son m=14 (y n=20) o m=20 (y
n=14). En cualquier caso, el número de alumnos es
14x20=280.
Problema 2
Llamemos A, B, C, D, E y F a los
puntos. Trabajaremos por casos:
Caso 1: De algún punto, que supondremos sin
pérdida de generalidad que es A, salen 5 distancias
1.
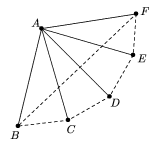
Entre B, C, D, E y F hay
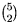 =10 distancias, así que alguna de
éstas es unitaria pues, en caso contrario sólo habría
5 distancias unitarias ya que el total de distancias es =10 distancias, así que alguna de
éstas es unitaria pues, en caso contrario sólo habría
5 distancias unitarias ya que el total de distancias es
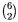 =15. Los extremos de
este segmento junto con el punto A forman el triángulo
equilátero (si, por ejemplo, el segmento unitario fuera BC,
entonces ABC sería el triángulo buscado). =15. Los extremos de
este segmento junto con el punto A forman el triángulo
equilátero (si, por ejemplo, el segmento unitario fuera BC,
entonces ABC sería el triángulo buscado).
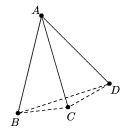
Caso 2: De algún punto salen sólo 4
distancias 1.
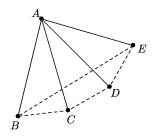
Entre B, C, D y E hay 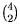 =6 distancias. Si ninguna de estas 6
distancias es unitaria, entonces las otras 4
distancias unitarias salen del punto F y van a dar a B,
C, D y E, pero el único punto que puede estar
a distancia 1 de B, C, D, E es
A, (pues A es el centro del círculo que pasa
por ellos) luego F=A, lo cual es una contradicción. Entonces
entre las 6 distancias hay una unitaria y los extremos de este
segmento junto con el punto A forman el triángulo buscado. =6 distancias. Si ninguna de estas 6
distancias es unitaria, entonces las otras 4
distancias unitarias salen del punto F y van a dar a B,
C, D y E, pero el único punto que puede estar
a distancia 1 de B, C, D, E es
A, (pues A es el centro del círculo que pasa
por ellos) luego F=A, lo cual es una contradicción. Entonces
entre las 6 distancias hay una unitaria y los extremos de este
segmento junto con el punto A forman el triángulo buscado.
Caso 3: De algún punto salen sólo 3
distancias
1.
Si una de BC, CD o DB es 1, terminamos.
Supongamos que ninguna es 1; entonces las restantes 5
distancias unitarias salen de E o F.
Entonces en el pentágono BCDEF hay 5 distancias
unitarias y BC, CD y DB no lo son. Si de E
tuviera distancia 1 con tres de B, C o D entonces
E=A, así que E a lo más tiene dos distancias 1
con B, C y D, y lo mismo ocurre con F. Como
falta una distancia 1, entonces ésta debe ser entre E y
F. Tenemos que de cada uno de E y F salen dos
distancias unitarias que van a los vértices B, C,
D, luego a alguno de estos vértices, por ejemplo C,
llegan dos distancias unitarias y así el triángulo buscado
es CEF.
Finalmente observemos que siempre se está en un caso de los
anteriores, pues si de ningún vértice no salieran
más de dos distancias unitarias, entonces a lo más
habría 6 distancias 1.
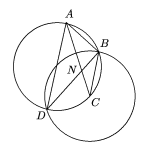
Problema 3
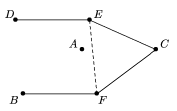
Primera demostración.
Como los arcos BC y CD son iguales, los ángulos
 DAC y DAC y  BDC son
iguales y, puesto que BDC son
iguales y, puesto que  ACD = ACD =  NCD es común para los triángulos
NCD es común para los triángulos
 ACD y ACD y
 DCN,
tenemos que estos dos triángulos son semejantes.
Luego AC/CD=CD/NC, pero
CD=CL, y así tenemos
que AC/CL=CL/NC. DCN,
tenemos que estos dos triángulos son semejantes.
Luego AC/CD=CD/NC, pero
CD=CL, y así tenemos
que AC/CL=CL/NC.
Esto, junto con el hecho de que el ángulo  ACL es
común para los triángulos ACL es
común para los triángulos  ACL y ACL y  LCN,
nos garantiza que estos triángulos son semejantes. Pero LCN,
nos garantiza que estos triángulos son semejantes. Pero  ACL es un triángulo
rectángulo, luego ACL es un triángulo
rectángulo, luego
 LCN también es
rectángulo
con ángulo recto en N, por lo que LN es perpendicular
a AC.
También, como CD=CM, tenemos que
AC/CM=CM/NC, y
de manera análoga se llega a que MN es perpendicular a
AC.
Luego L , M y N son colineales. LCN también es
rectángulo
con ángulo recto en N, por lo que LN es perpendicular
a AC.
También, como CD=CM, tenemos que
AC/CM=CM/NC, y
de manera análoga se llega a que MN es perpendicular a
AC.
Luego L , M y N son colineales.
Segunda demostraci\'on.
Tenemos que  ADB = ADB =  DAC = DAC =
 CAB = CAB =  DBC = DBC =
 ACB=pi/7 ya que AB,
BC y CD son lados de un heptágono regular. Luego
los triángulos ACB=pi/7 ya que AB,
BC y CD son lados de un heptágono regular. Luego
los triángulos  ABC
y ABC
y  BNC son isósceles
y con los ángulos iguales y, por tanto, son semejantes.
Entonces CA/CB=CB/CN,
lo que implica que CNxCA=CB2. (*) BNC son isósceles
y con los ángulos iguales y, por tanto, son semejantes.
Entonces CA/CB=CB/CN,
lo que implica que CNxCA=CB2. (*)
De aquí hay dos formas para continuar:
Primera forma. Como CL es igual a CB,
la ecuación (*) se reescribe como CNxCA=CL2,
lo cual implica que
CA/CL=CL/CN;
esto, junto con el hecho de que en los triángulos  CNL y CNL y  CLA el
ángulo en C es común, nos dice que los dos
triángulos son semejantes (por el criterio de semejanza
(LAL)). Como CLA el
ángulo en C es común, nos dice que los dos
triángulos son semejantes (por el criterio de semejanza
(LAL)). Como  CLA
es
rectángulo, también lo es el CLA
es
rectángulo, también lo es el  CNL, y entonces LN es
perpendicular a CA.
Análogamente se puede llegar a ver que MN es perpendicular a
CA, luego L, M y N son colineales. CNL, y entonces LN es
perpendicular a CA.
Análogamente se puede llegar a ver que MN es perpendicular a
CA, luego L, M y N son colineales.
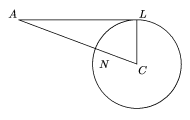
Segunda forma. La ecuación (*) nos garantiza que
N y A son puntos inversos con respecto a la circunferencia
de centro C y radio CB., y una forma de encontrar el inverso
de A con respecto a tal circunferencia es trazar las tangentes
desde A a la circunferencia y unir los puntos de tangencia L
y M, entonces la intersección de LM con CA es
el inverso, luego N se encuentra sobre la línea
LM.
Problema 4
(a) Un posible conjunto B es el que consta del 1, de
todos los primos del conjunto A, de todos los productos que caen en
A de dos de estos primos y del único producto de tres de
estos primos que pertenecen a A:
B
=
{1,
2,
3,
5,
7,
11,
13,
17,
19, 23,
29, 31, 2x3, 2x5, 2x7, 2x11, 2x13, 2x17,
2x19, 3x5, 3x7, 3x11, 3x13, 5x7, 2x3x5}.
Para convencernos que el conjunto dado cumple la propiedad observemos
que dados dos elementos a y b en B diferentes de
1, en las factorizaciones de a y b aparecen
únicamente primos elevados a la potencia 1, y, como a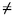 b, entonces en uno de ellos aparece un primo
p que no aparece en el otro y así su producto ab, el
primo p aparece a la potencia 1, lo cual muestra que
ab no es un cuadrado perfecto.
Nótese también que, 1 x a = a no es un cuadrado
perfecto.
Por tanto ningún producto de dos elementos de B es un
cuadrado
perfecto. b, entonces en uno de ellos aparece un primo
p que no aparece en el otro y así su producto ab, el
primo p aparece a la potencia 1, lo cual muestra que
ab no es un cuadrado perfecto.
Nótese también que, 1 x a = a no es un cuadrado
perfecto.
Por tanto ningún producto de dos elementos de B es un
cuadrado
perfecto.
(b) Observemos que un conjunto con las características pedidas
deberá
tener a lo más un elemento de cada uno de los siguientes conjuntos
(pues en cada uno de ellos el producto de cualesquiera dos elementos es
un cuadrado):
{1,4,9,16,25,36} es decir los cuadrados,
{2,8,18,32} es decir, los de la forma 2x2,
{3,12,27} es decir, los de la forma 3x2,
{5,20} es decir, los de la forma 5x2,
{6,24} es decir, los de la forma 6x2,
{7,28} es decir, los de la forma 7x2 y
{10,40} es decir, los de la forma 10x2.
Entonces, para formar un conjunto B con las condiciones pedidas,
habrá que empezar por eliminar todos menos tal vez uno de
los elementos de cada uno de esos
conjuntos y el conjunto buscado tendrá como máximo
40-5-3-2-1-1-1-1=26. elementos. Por tanto no puede existir un
conjunto con 27 elementos que cumpla lo que se pide en el inciso (a).
Problema 5
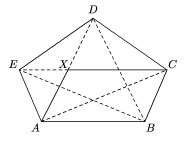
Si las áreas de los triángulos  ABC y ABC y  BCD
son iguales, como tienen la misma base BC,
entonces las alturas son iguales y así los vértices A
y D se encuentran sobre una línea paralela a BC, es
decir AD || BC.
Por la misma razón, como las áreas de los triángulos BCD
son iguales, como tienen la misma base BC,
entonces las alturas son iguales y así los vértices A
y D se encuentran sobre una línea paralela a BC, es
decir AD || BC.
Por la misma razón, como las áreas de los triángulos
 EAB y EAB y  ABC
son iguales se tiene que AB || CE; lo anterior implica que
ABCX es un paralelogramo, donde X
es la intersección de AD y CE. En el paralelogramo
ABCX, es claro que las áreas de los triángulos ABC
son iguales se tiene que AB || CE; lo anterior implica que
ABCX es un paralelogramo, donde X
es la intersección de AD y CE. En el paralelogramo
ABCX, es claro que las áreas de los triángulos
 ABC y ABC y
 ACX son iguales. ACX son iguales.
También observemos que el área del  AXE es estrictamente menor que el
área del AXE es estrictamente menor que el
área del
 DEA (la base AX es
estrictamente
menor que la base AD y ambos tienen la misma altura sobre tales
bases).
Finalmente se tiene que el área del DEA (la base AX es
estrictamente
menor que la base AD y ambos tienen la misma altura sobre tales
bases).
Finalmente se tiene que el área del  ACE es mayor que el área
del triángulo ACE es mayor que el área
del triángulo  ACX (la base AE del ACX (la base AE del
 ACE es mayor que la base
AX del ACE es mayor que la base
AX del  ACX y ambos tienen la misma
altura sobre esta
base). ACX y ambos tienen la misma
altura sobre esta
base).
Si (XYZ...) denota el área de la figura XYZ...
tenemos:
(ABCDE) = (ABC) +(ACX) +(CDE) +(EAX)
= 3(ABC) + (EAX) < 4(ABC)
por tanto
1/4(ABCDE) < (ABC)
y también
(ABCDE) = (ABC) + (CDE) + (EAC) > 3(ABC)
y de aquí que
(ABC) < 1/3(ABCDE)
Problema 6
Consideremos un arreglo arbitrario de 0's y
1's. Veremos en qué cuadros se pueden lograr
0's sin afectar el resto de los cuadros. Como
hay diagonales que pasan sólo por cada esquina,
en las esquinas siempre se pueden lograr 0's sin
afectar lo demás.
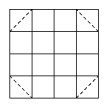
También, como hay diagonales que pasan sólo por uno de
los cuadros centrales, en los cuadros centrales siempre se pueden lograr
0's.
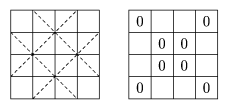
A partir de aquí trabajaremos sólo en los cuadros
centrales
de las columnas y renglones exteriores mediante operaciones en esas
columnas y renglones y en las diagonales de longitud dos; de esta
manera el centro se mantendrá sin cambio y las esquinas, como
dijimos arriba, siempre pueden volver a hacerse 0's sin
cambiar lo demás.
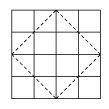
Si en uno de los renglones o columnas de la orilla hay dos 1's
centrales, éstos podemos convertirlos en 0's y lo
mismo ocurre si hay dos 1's contiguos en una diagonal de
longitud dos.
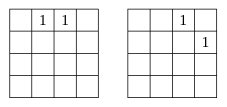
Por otro lado, si en una diagonal de longitud dos hay un 0 y un 1,
éstos podemos intercambiarlos. Por estas observaciones, podemos
"bajar" todos los 1's que haya en el arreglo hasta el
renglón inferior. Aquí tenemos dos casos, que nos queden dos
1's, en cuyo caso podemos convertirlos en 0's, y que nos
quede un solo 1.
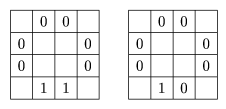
Finalmente observemos que cualquiera de las operaciones
mantiene la paridad del número de 1's en los cuadros
centrales de las columnas y renglones exteriores; es decir, si
había un número par de 1's en estas posiciones,
por más operaciones que se apliquen, el número de
1's se mantendrá par y también se mantendrá
impar si en un principio era impar.
Entonces tenemos que una posición se puede llevar a puros
0's si y sólo si el número de unos en los cuadros
centrales de las orillas es par.
|







