Cuarta Olimpiada Matemática de
Centroamérica y el Caribe
Mérida, México, julio 2 y 3 de
2002
Primer Día
Problema 1.
¿Para qué enteros n
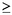3 es
posible acomodar, en algún orden, los números
1, 2, ..., n en forma circular de manera que cualquier
número divida a la suma de los dos números siguientes en el
sentido de las manecillas del reloj?
Problema 2.
Sea ABC un triángulo acutángulo y sean D y E los pies de las alturas desde los vértices A y B, respectivamente. Muestre que si
área(DEA)
área(EAB)
área(ABD)
entonces el triángulo es isósceles.
Problema 3.
Para cada entero a > 1 se construye una lista infinita de enteros L(a) como sigue:
- a es el primer número de la lista L(a)
- Dado un número b en L(a), el siguiente número en la lista es b+c, donde c es el mayor entero que divide a b y es menor que b.
Segundo Día
Problema 4.
Sean ABC un triángulo, D el punto medio de BC, E un punto sobre el segmento AC tal que BE=2AD y F el punto de intersección de AD con BE. Si el ángulo DAC mide 60o, encuentre la medida de los ángulos del triángulo FEA.
Problema 5.
Encuentre un conjunto infinito de enteros positivos S tal que para cada n
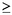1 y cualesquiera n elementos
distintos x1,x2,...,xn de
S,
el número x1 + x2 + ... +
xn no es un cuadrado perfecto.
Problema 6.
En el plano coordenado se tiene la cuadrícula de n
n, con n entero mayor o igual que 2, cuyos
vértices son los puntos (x,y), con x y y
enteros que cumplen 0xn y 0yn. Considere los caminos que van de (0,0)
a (n,n) sobre las líneas de esta cuadrícula y que
sólo avanzan hacia la derecha o hacia arriba. Uno de tales caminos
se llama equilibrado si la suma de los valores de x de todos
los puntos por los que pasa es igual a la suma de todos los valores de
y de esos mismos puntos. Muestre que todo camino equilibrado divide
al cuadrado de lado n en dos figuras de la misma área.