



 |
 |
 |
|
 |
|||
|
|
Morelia, Michoacán, noviembre de 2000 |
| a | b | c | d | ... | ||||
| a+b | b+c | c+d | ... | |||||
| a+2b+c | b+2c+d | ... | ||||||
| a+3b+3c+d | ... |
Con este esquema es claro que los coeficientes que van
apareciendo son los números del triángulo de
Pascal, así que el
número
buscado es:
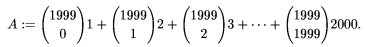
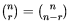 , así que podemos factorizar y
, así que podemos factorizar y
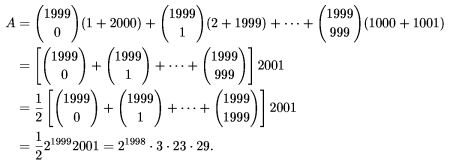
La respuesta es 3. Veamos primero que si A tiene dos elementos, entonces en A'' no pueden estar todos los números del 1 al 40:
Primera forma. Sea A = {a,b} con a>b; entonces
A' = {a,b,a-b,a+b}, y los elementos de A''
son los enteros positivos de la forma: pa+qb+r(a-b)+s(a+b) con
p,q,r,s 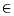 {-1,0,1}, así que el
número
de elementos de A'' es menor o igual que
34-1/2 (pues el 0 no debe
considerarse y
hay tantos números positivos como negativos); sin embargo,
a+b se obtiene de dos maneras distintas, así que A''
no puede tener 40 elementos.
{-1,0,1}, así que el
número
de elementos de A'' es menor o igual que
34-1/2 (pues el 0 no debe
considerarse y
hay tantos números positivos como negativos); sin embargo,
a+b se obtiene de dos maneras distintas, así que A''
no puede tener 40 elementos.
Segunda forma. Sea A como en la primera forma y sea
B el conjunto de enteros (positivos, negativos o cero) que se
obtienen escogiendo uno o más elementos de A'',
poniéndole el signo + o el signo - a cada uno y
sumando
los números con signo. Probaremos que B tiene a lo
más 37
elementos. Los elementos de B son de la forma ka+lb con
|k|,|l| 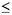 3. Es
fácil ver que si
|k| = 3, entonces |l| = 0 o 1;
análogamente si |l| = 3, entonces |k| = 0
o 1. Por lo tanto, (|k|,|l|) no puede ser
(2,3), (3,2) o (3,3). Para (|k|,|l|) = (0,0) hay una sola pareja
(k,l). Si
(|k|, |l|) es una de las 6 parejas: (1,0),
(2,0), (3,0), (0,1), (0,2) o (0,3); hay dos valores posibles
de (k,l). Para cada uno de los otros 6 valores de
(|k|, |l|) hay cuatro posibilidades para
(k,l). Por lo tanto, hay a lo más 1 + 2 x 6 + 4 x 6 =
37 números en B.
3. Es
fácil ver que si
|k| = 3, entonces |l| = 0 o 1;
análogamente si |l| = 3, entonces |k| = 0
o 1. Por lo tanto, (|k|,|l|) no puede ser
(2,3), (3,2) o (3,3). Para (|k|,|l|) = (0,0) hay una sola pareja
(k,l). Si
(|k|, |l|) es una de las 6 parejas: (1,0),
(2,0), (3,0), (0,1), (0,2) o (0,3); hay dos valores posibles
de (k,l). Para cada uno de los otros 6 valores de
(|k|, |l|) hay cuatro posibilidades para
(k,l). Por lo tanto, hay a lo más 1 + 2 x 6 + 4 x 6 =
37 números en B.
Ahora veamos que con tres sí se puede:
Primera forma. Sea A = {4,13,14}; entonces A' contiene a {1,3,32,33}, y es fácil ver que A'' contiene a todos los números del 1 al 1+3+32+33 = 40.
Segunda forma. Observemos
primero que si X = {1,2,...,n}, entonces X' contiene
a todos los números del 1 al 1+2+...+n (pues en
X'
están: n+1,..., n+(n-1), n+(n-1)+1, ...,
n+(n-1)+(n-2),..., n+(n-1)+(n-2)+... +1);
por tanto, como queremos que A'' contenga
del 1 al 40, entonces bastaría con que A'
contuviera a
todos los
números del 1 al 9. Entonces, por lo mismo,
bastaría que
A
contuviera a los números del 1 al 4; así que
con cuatro sí
es posible.
Sin embargo, es claro que hay muchas repeticiones al construir
A', así que busquemos ver si con tres se puede, evitando
repeticiones: En A ponemos al 1 y después no ponemos
al 2 (pues su diferencia con 1 es 1, que ya está); ponemos
al 3; no ponemos al 4 (pues 4-3 = 1), ni tampoco al
5
(pues 5-3 = 3-1), no ponemos al
6 (pues 6-3 = 3); entonces intentamos con el 7. Ahora
comprobamos (fácilmente) que con A = {1,3,7}, en A'
obtenemos todos los números del 1 al 9, y ya
terminamos.
Problema 4
El máximo es 5. El k-ésimo
número construido es 5ak-1 + (ak-2 +
ak-3 + ... + 1)b,
como puede comprobarse fácilmente. Si a no es congruente con
1
módulo 5, entonces
a3+a2+a+1
= (a4-1)/(a-1),
es múltiplo
de 5. (Nota: Esto se puede hacer sin usar congruencias
analizando el último dígito de a). Entonces en este
caso el quinto número es múltiplo de 5 y mayor que 5,
así que no es primo. Si a 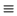 1 mod
5, entonces a4+a3+a2+a +1 es
múltiplo de 5 así que el sexto número no es
primo. Por otro lado, para a = 1 y b = 6 los primeros 5
números obtenidos son todos primos: 5, 11, 17, 23, 29.
1 mod
5, entonces a4+a3+a2+a +1 es
múltiplo de 5 así que el sexto número no es
primo. Por otro lado, para a = 1 y b = 6 los primeros 5
números obtenidos son todos primos: 5, 11, 17, 23, 29.
Problema 5
Es claro que para n = 2 es imposible. Veamos que es posible para toda n>2. Tomemos primero el caso n impar. Eligiendo los rectángulos de 1 x n cambiemos el color de todos los renglones en posición impar. De esta manera todas las columnas en posición impar quedan blancas y todas las columnas en posición par quedan negras; entonces con rectángulos de n x 1 cambiamos las columnas en posicón par para lograr que todos los cuadros sean blancos.
Para ver el caso cuando n = 2ab, donde a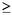 1 y b
impar distinto de 1, subdividamos el tablero en tableros de b x b
y hagamos en cada tablero de b x b las operaciones que indicamos en el
caso n impar.
1 y b
impar distinto de 1, subdividamos el tablero en tableros de b x b
y hagamos en cada tablero de b x b las operaciones que indicamos en el
caso n impar.
Nos falta analizar las potencias de 2. Por un argumento
similar al que describimos en el caso anterior, basta analizar el caso
n = 4, el cual indicamos en los siguientes dibujos, en los que, en
cada paso, se ha escogido un rectángulo de 2 x 4
o de 4 x 2 para hacer la operación:

Notemos que  BAH =
BAH =  ABH =
ABH =
 BHF =
BHF =  FHC =
FHC =
 HFD =
HFD =  FDB =
FDB = 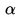 , pues ABH es isósceles,
HF es
paralela a AB y DE es paralela a AC. Entonces, el
cuadrilátero
HDBF es cíclico y como
, pues ABH es isósceles,
HF es
paralela a AB y DE es paralela a AC. Entonces, el
cuadrilátero
HDBF es cíclico y como  HDB es
recto
(ABH es
isósceles), tenemos que
HDB es
recto
(ABH es
isósceles), tenemos que  HFB es
recto. Por
lo tanto,
HFB es
recto. Por
lo tanto,
 DBF es recto (pues DB || HF). Como
DBF es recto (pues DB || HF). Como
 HBE también es
recto,
HBE también es
recto,  FBE =
FBE =  DBH =
DBH =
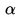 .
.
Primera forma Sea G la intersección de BF y AC. Los triángulos ABC y BGC son semejantes (tienen dos ángulos iguales). Notemos que como DE es la recta de los puntos medios, F es el punto medio de BG, de modo que CF es mediana de BGC. Los ángulos BCF y ACD son ángulos correspondientes (entre un lado y una mediana) en triángulos semejantes y por lo tanto son iguales.
Segunda forma. Sean I y J las intersecciones de
HF
con CD y BC respectivamente. De lo anterior,
 FBC =
FBC =  IHC. Para ver que
son
semejantes los tri\'angulos FBC y IHC (lo cual nos da
directamente
el resultado) sólo falta probar que
FB/IH = BC/HC.
Es claro que I es el punto medio de HJ pues HJ || AB
y D es el punto medio de AB. Como HBJ es un
triángulo rectángulo, lo anterior quiere decir que I
es su circuncentro y por lo tanto, IH = IB. También, IBF
IHC. Para ver que
son
semejantes los tri\'angulos FBC y IHC (lo cual nos da
directamente
el resultado) sólo falta probar que
FB/IH = BC/HC.
Es claro que I es el punto medio de HJ pues HJ || AB
y D es el punto medio de AB. Como HBJ es un
triángulo rectángulo, lo anterior quiere decir que I
es su circuncentro y por lo tanto, IH = IB. También, IBF
 HCB pues ambos son triángulos
rectángulos y
HCB pues ambos son triángulos
rectángulos y
 BHC = 2
BHC = 2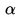 =
=  BIF. Por lo tanto,
FB/IH = FB/IB=
BC/HC, que es lo que faltaba probar.
BIF. Por lo tanto,
FB/IH = FB/IB=
BC/HC, que es lo que faltaba probar.