|
|
Décima Cuarta Olimpiada Nacional de
Matemáticas
Morelia, Michoacán, noviembre de 2000
Primer Día
Problema 1.
Sean 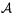 , , 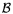 , ,  y y
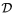 circunferencias tales que circunferencias tales que 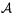 es
tangente
exteriormente a es
tangente
exteriormente a 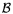 en P, en P, 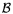 es
tangente
exteriormente a
es
tangente
exteriormente a  en Q, en Q,  es
tangente
exteriormente a
es
tangente
exteriormente a 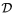 en R y en R y 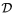 es
tangente
exteriormente a
es
tangente
exteriormente a 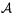 en S. Supón que en S. Supón que
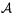 y
y  no se intersectan, ni tampoco no se intersectan, ni tampoco 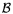 y
y 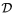 . .
(i) Prueba que los puntos P, Q R y S
están todos
sobre una circunferencia.
(ii) Supón además que 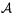 y y  tienen
radio 2, tienen
radio 2, 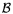 y y 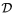 tienen radio 3 y la
distancia entre
los centros de tienen radio 3 y la
distancia entre
los centros de 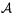 y y  es 6.
Determina el área del
cuadrilátero PQRS. es 6.
Determina el área del
cuadrilátero PQRS.
Problema 2.
Se construye un tríangulo como el de la figura, pero empezando con
los números del 1 al 2000. Cada número del triángulo
-excepto los del primer renglón- es la suma de los dos
números
arriba de él. ¿Cuál es el número que ocupa el
vértice
inferior del triángulo? (Nota: Escribe tu respuesta final
como producto de primos.)
| 1 |
|
2 |
|
3 |
|
4 |
|
5 |
| |
3 |
|
5 |
|
7 |
|
9 |
|
| |
|
8 |
|
12 |
|
16 |
|
|
| |
|
|
20 |
|
28 |
|
|
|
| |
|
|
|
48 |
|
|
|
|
Problema 3.
Dado un conjunto A de enteros positivos, construimos el
conjunto A' poniendo todos los elementos de A y todos los
enteros positivos que se pueden obtener de la siguiente manera: Se
escogen algunos elementos de A, sin repetir, y a cada uno de esos
números se le pone el signo + o el signo -; luego se
suman esos
números con signo y el resultado se pone en A'. Por
ejemplo, si A={2,8,13,20}, entonces algunos elementos de
A' son 8 y 14 (pues 8 es elemento de A
y 14=20+2-8). A partir de A' construimos
A'' de la misma manera que A' se construye a
partir de A. Encontrar el mínimo
número de elementos que necesita tener A si queremos que
A'' contenga a todos los enteros
del 1 al 40 (inclusive).
Segundo Día
Problema 4.
Para a y b enteros positivos no múltiplos de
5, se
construye una lista de números como sigue: El primer número
es 5 y, a partir del segundo número, cada número se
obtiene
multiplicando el número que le precede (en la lista) por a y
sumándole b. (Por ejemplo, si a=2 y b=4,
entonces los primeros tres números de la lista serían:
5,
14, 32 (pues
14=(5x2)+4 y 32=(14x2)+4). ¿Cuál es la
máxima
cantidad
de primos que se pueden obtener antes de obtener el primer número
no primo?
Problema 5.
Se tiene un tablero de n x n pintado como tablero de
ajedrez. Está permitido efectuar la siguiente operación en
el tablero: Escoger un rectángulo en la cuadrícula tal que
las longitudes de sus lados sean ambas pares o ambas impares, pero que no
sean las dos iguales a 1 al mismo tiempo, e invertir los colores de los
cuadritos de ese rectángulo (es decir, los cuadritos del
rectángulo que eran negros se convierten en blancos y los que eran
blancos, se convierten en negros). Encuentra para qué n's
es
posible lograr que todos los cuadritos queden de un mismo color
después de haber efectuado la operación el número de
veces que sea necesario. (Nota: Las dimensiones de los rectángulos
que se escogen pueden ir cambiando.)
Problema 6.
Sea ABC un triángulo en el que  B>90o y en el que un punto H sobre AC
tiene la
propiedad de que
AH = BH, y BH es perpendicular a BC. Sean D y
E los puntos medios de AB y
BC, respectivamente. Por H se traza una paralela a AB
que corta a DE en F.
Prueba que
B>90o y en el que un punto H sobre AC
tiene la
propiedad de que
AH = BH, y BH es perpendicular a BC. Sean D y
E los puntos medios de AB y
BC, respectivamente. Por H se traza una paralela a AB
que corta a DE en F.
Prueba que  BCF = BCF =  ACD.
ACD.
|








 B>90o y en el que un punto H sobre AC
tiene la
propiedad de que
AH = BH, y BH es perpendicular a BC. Sean D y
E los puntos medios de AB y
BC, respectivamente. Por H se traza una paralela a AB
que corta a DE en F.
Prueba que
B>90o y en el que un punto H sobre AC
tiene la
propiedad de que
AH = BH, y BH es perpendicular a BC. Sean D y
E los puntos medios de AB y
BC, respectivamente. Por H se traza una paralela a AB
que corta a DE en F.
Prueba que  BCF =
BCF =  ACD.
ACD.