Para p = 5 tenemos que 8p⁴-3003 = 1997, que es primo. Ahora veamos que es la única posibilidad. Sea p un número primo distinto de 5 y supongamos que 8p⁴-3003 es primo. Podemos proceder de dos maneras: Tenemos que 8p⁴-3003 3p⁴-3 3(p⁴-1) (mod 5),

Pero p⁴-1 0 (mod 5) para cualquier primo p 5 (esto se comprueba fácilmente analizando los posibles residuos de p), así que 8p⁴-3003 es divisible entre 5 y, como estamos suponiendo que es primo, la única posibilidad es 8p⁴-3003 = 5, lo cual es un absurdo pues ³⁰⁰⁸/₈ = 376 que no tiene raíz cuarta entera.

Nota: Se puede evitar el lenguaje de las congruencias, observando que si p es un primo distinto de 2 y de 5, entonces p termina en 1, 3, 7 o 9, así que p⁴ termina en 1 y, por tanto, 8p⁴-3003 termina en 5, lo cual lo hace forzosamente múltiplo de 5. El caso p = 2 se puede tratar aparte (viendo que 8(2)⁴-30030 o que también 2⁴ termina en 6, así que 8p⁴-3003 también termina en 5.


Problema 2

Usando el teorema de Tales tenemos que QP' || AB, puesto que estos segmentos están cortados por las transversales CA y CB, y se tiene que ^CQ/_QA=^CP'/_P'B. Entonces los triángulos CQP' y CAB son semejantes con razón de semejanza ^CQ/_QA; de aquí que QP'=AR. Tenemos entonces que los triángulos AKR y P'KQ son iguales, de donde K es el punto medio de AP'. Sea M el punto medio de BC.

APP'

(i) A continuación se muestra una posibilidad para acomodar los números de manera que en cuadros adyacentes la diferencia de los números que aparecen es menor o igual a 4.

(ii) Supongamos que sí es posible colocar los números y analicemos cómo deben estar acomodados. En la lista de seis números 1,4,7,10,13,16, entre dos números consecutivos hay una diferencia de 3, de manera que en cualquier colocación de los números en la cuadrícula de 4 x 4 en la que las diferencias en casillas adyacentes fueran menores o iguales que 3, los números 1 y 16 deberían estar a una separación de, por lo menos, 6 casillas; esto sólo es posible si uno está en una esquina y el otro en cualquiera de los tres cuadritos de la esquina opuesta. Supongamos, sin pérdida de generalidad, que 1 aparece en la esquina superior izquierda; entonces el 16 debe quedar en cualquiera de las 3 casillas más lejanas, como se indica en el esquema siguiente.

Supongamos que 16 no aparece en la esquina. Esto forzaría a que en cualquier "camino" que usara seis casillas adyacentes entre los cuadritos donde se encontraran el 1 y el 16, aparecieran exactamente los números de la lista; sin embargo, hay más de un camino entre las dos casillas (ver el ejemplo en la figura, abajo), lo que forzaría a que hubiera repetición de números.

Entonces, el 16 aparece en la esquina inferior derecha. Ahora observemos que en dos cuadritos diagonales que compartan un vértice, la diferencia máxima que puede haber es de 5, puesto que, sumando las diferencias por cuadros adyacentes la diferencia máxima debe ser 6, pero los números no pueden estar repetidos. Como del 1 al 16 se llega en 4 pasos con diferencias de 5: 1-6-11-16, la única posibilidad es que estos números queden en la diagonal, como se indica en la figura abajo. Además, en las casillas adyacentes al 1 deben aparecer el 3 y el 4, puesto que con ambos 1 y 6 la diferencia debe ser a lo más 3. Sin pérdida de generalidad aparecen como en el esquema.

Entonces las casillas que sobran para acomodar el 2 quedan todas a una distancia a lo más de 4 de la casilla donde está el 16; sin embargo, para llegar del 2 al 16 con diferencias a lo más de 3 se necesitan por lo menos 4 números intermedios, así que no es posible la colocación.


Problema 4

Supongamos que tenemos 6 puntos no coplanares en el espacio de manera que no hay tres alineados. Tenemos varios casos:

(I) Si 5 de ellos son coplanares. Entonces estos determinan un plano y el otro punto determina un plano más con cada pareja de los coplanares; como son 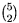=10 parejas, en total se determinan 11 planos.

(II) Si no hay 5 coplanares pero sí 4. Sean A, B, C y D los cuatro puntos coplanares, sea 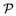el plano que determinan y sean X y Y los otros puntos. Tenemos tres subcasos:

(IIa) Si X y Y no son coplanares con ninguna pareja de A, B, C y D. Entonces cada pareja de A, B, C y D determina un plano con cada uno de X y Y y además tenemos 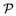, así que en este caso se determinan por lo menos 1+2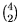= 13 planos.

(IIb) Si X y Y son coplanares con exactamente una de las parejas de A, B, C y D, digamos con (A,B). Entonces tenemos 2+2 [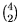-1]=12 planos, pues cada uno de X y Y determina un plano con cada una de las parejas de A, B, C y D distintas de (A,B) (esto es, tenemos los planos: (A,B,C,D), (X,Y,A,B), (X,A,C), (X,A,D), (X,B,C), (X,B,D), (X,C,D), (Y,A,C), (Y,A,D), (Y,B,C), (Y,B,D) y (Y,C,D)).

(IIc) Si X y Y son coplanares con dos de las parejas de A, B, C y D. Observemos que las parejas deben ser ajenas, pues X y Y no pertenecen a 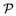. Sin pérdida de generalidad, las parejas son (A,B) y (C,D). Este caso es como el anterior sólo que aquí hay un plano repetido: (X,C,D) coincide con (Y,C,D), así que en este caso son 11 planos.

(III) Si no hay 4 coplanares. En este caso, cada terna determina un plano, así que son 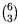=20.

Hemos analizado todos los casos y con ello probado que el menor número de planos posible es 11.


Problema 5

Presentaremos aquí dos soluciones. En ambas denotaremos por (XYZ) el área de un triángulo XYZ.

Primera Solución. Observemos primero que el ABC se parte en los 7 triángulos de la misma área que se indican en la figura. (Por ejemplo, (AB'A') =(AA'C) pues B'A'=A'C y la altura en A es la misma.)

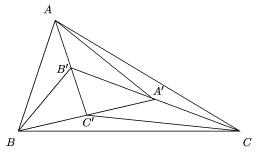
Construyamos un paralelogramo BLAC', como se indica en la figura.

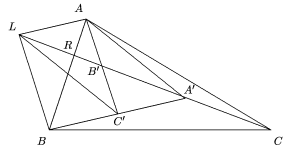
Entonces, como LA=BC' =C'A', también LAA'C' es paralelogramo, así que sus diagonales se intersectan en el punto medio que es B' (pues AB'=B'C'). También las diagonales de LABC' se intersectan en su punto medio, así que en el ALC', AR es mediana, pero como también lo es LB', tenemos que R es centroide de este triángulo, de donde RB' =¹/₃ LB'=¹/₃ B'A'. Análogamente, C'P=¹/₃B'C' y A'Q=¹/₃C'A'. Partamos PQR como se indica.

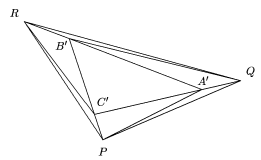
Como antes, los triángulos RB'C', PA'C' y QA'B' tienen área ¹/₃(A'B'C') y los triángulos PRC', PQA' y RQB' tienen área 1/9 (A'B'C'). Entonces (PQR) = (A'B'C')+3 (¹/₃ (A'B'C')) + 3(¹/₉ (A'B'C')) = ⁷/₃ (A'B'C') = ⁷/₃ x ¹/₇ (ABC) = ¹/₃ (ABC).

Segunda Solución.- Aplicando Menelao al triángulo ABC' y a la recta RA' tenemos que -1= ^AR/_RB x ^BA'/_A'C' x ^C'B'/_B'A = ^AR/_RB x (-2) x 1,

de donde ^AR/_RB =¹/₂; por tanto AR=¹/₃ AB. Análogamente AQ=²/₃ AC.

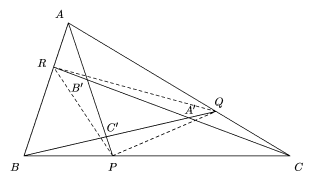
Ahora, (ARQ)= ¹/₂(AQ x AR x sen A) =¹/₃ AB x ²/₃ AC x sen A x ¹/₂ =²/₉(ABC). Análogamente, (PQC)=²/₉ (ABC) y (BRP)=²/₉(ABC). Entonces (PQR)= (1- 3 x ²/₉)(ABC) =¹/₃ (ABC).


Problema 6

Observemos que si n es cualquier natural, entonces ¹/_n - ¹/_n+1 = ¹/_n(n+1) , de donde

Usando esto y que ¹/₂ + ¹/₃ + ¹/₆=1, podemos hacer sustituciones (¹/₂ por ¹/₃ + ¹/₆, ¹/₃ por ¹/₄ + ¹/₁₂ y ¹/₆ por ¹/₇ + ¹/₄₂, para obtener una nueva expresión en la que los denominadores son más grandes. Luego podemos repetir el procedimiento hasta lograr una expresión en la que el denominador más chico sea 5 y no haya repetidos: (¹/₃ + ¹/₆) + (¹/₄ + ¹/₁₂) + (¹/₇ + ¹/₄₂)=1, (¹/₄ + ¹/₁₂)+ (¹/₇ + ¹/₄₂) + (¹/₅ + ¹/₂₀ ) + (¹/₁₃ + ¹/₁₅₆) + (¹/₈ + ¹/₅₆) + (¹/₄₃ + ¹/ ₁₈₀₆)=1.

Ahora sólo sustituimos ¹/₄, ¹/₅ y ¹/₂₀ y los ordenamos: ¹/₅+¹/₆+ ¹/₇ + ¹/₈ + ¹/₁₂ + ¹/₁₃ + ¹/₂₀ + ¹/₂₁ + ¹/₃₀ + ¹/₄₂ + ¹/₄₃ + ¹/₅₆ + ¹/₁₅₆ + ¹/₄₂₀ + ¹/₁₈₀₆ =1.

Hemos logrado entonces una expresión de las requeridas. Para probar que hay una infinidad, basta observar que al sustituir el término que tenga el denominador mayor (usando (*)), se obtienen denominadores aún mayores.