|
|
Décima Quinta Olimpiada Nacional de
Matemáticas
Oaxtepec, Morelos, noviembre de 2001
Primer Día
Problema 1.
Encuentra todos los números de 7 dígitos que son
múltiplos de 3 y de 7, y cada uno de cuyos dígitos es 3 o 7.
Problema 2.
Se tienen algunas pelotas de colores (son por lo menos tres colores), y
por lo menos tres cajas. Las pelotas se ponen en las cajas de manera que
no quede vacía ninguna caja y que no haya tres pelotas de colores
distintos que estén en tres cajas distintas. Prueba que hay una
caja tal que todas las paelotas que están fuera de ella son del
mismo color.
Problema 3.
En un cuadrilátero ABCD inscrito en una circunferencia
llamemos P al punto de intersección de las diagonales
AC y BD, y sea M el punto medio de CD. La
circunferencia que pasa por P y que es tangente a CD en
M corta a BD y a AC en los puntos Q y
R, respectivamente. Se toma un punto S sobre el segmento
BD de tal manera que BS = DQ. Por S se traza una
paralela a AB que corta a AC en un punto T. Prueba
que AT = RC.
Segundo Día
Problema 4.
Dados dos enteros positivos n y a se forma una lista de
2001 números como sigue: El primer número es a; a
partir del segundo cada número es el residuo que se obtiene al
dividir el cuadrado del anterior entre n. A los números de
la lista se les ponen los signos + y - alternadamente
empezando con +. Los números con signo así obtenidos
se suman y a esa suma se le llama suma final para n y a. ¿Para
qué enteros n 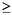 5 existe alguna
a tal que 2 5 existe alguna
a tal que 2 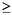 a a 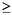 n/2 y la suma final para
n y a es positiva? n/2 y la suma final para
n y a es positiva?
Problema 5.
Sea ABC un triángulo tal que AB < AC y el
ángulo BAC es el doble del ángulo BCA. Sobre
el lado AC se toma un punto D tal que CD = AB. Por el
punto B se traza una recta 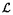 paralela a
AC. La bisectriz exterior del ángulo en A intersecta
a paralela a
AC. La bisectriz exterior del ángulo en A intersecta
a 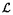 en el punto M, y la paralela a AB
por el punto C intersecta a en el punto M, y la paralela a AB
por el punto C intersecta a 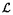 en el punto
N. Prueba que MD = ND. en el punto
N. Prueba que MD = ND.
Problema 6.
Un coleccionista de monedas raras tiene monedas de denominaciones 1, 2,
..., n (tiene muchas monedas de cada denominación). Desea poner
algunas de sus monedas en 5 cajas de manera que se cumplan las siguientes
condiciones:
- (a) En cada caja hay a lo más una moneda de cada
denominación.
- (b) Todas las cajas tienen el mismo número de monedas y la
misma cantidad de dinero.
- (c) Para cualesquiera dos cajas sucede que entre las dos tienen por lo
menos una moneda de cada denominación.
- (d) No existe una denominación tal que todas las cajas tengan
una moneda de esa denominación.
¿Para qué valores de n puede el coleccionista hacer lo
que se propone?
|







