

Segunda Olimpiada Matemática de Centroamérica y el
Caribe
Nueva San Salvador, El Salvador, julio 11 y 12 de
2000
Primer Día
Problema 1.
Encuentra todos los números naturales de tres dígitos abc (a
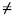 0), tales que a2
+ b2 + c2 es divisor de 26.
0), tales que a2
+ b2 + c2 es divisor de 26.
Problema 2.
Determina todos los enteros n
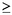 1 para los
cuales es posible construir un rectángulo de lados 15 y n, con
piezas congruentes a:
1 para los
cuales es posible construir un rectángulo de lados 15 y n, con
piezas congruentes a:
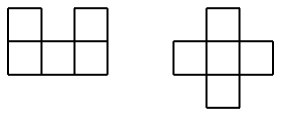
Notas:
- (a) Las piezas no deben superponerse ni dejar huecos.
- (b) Los cuadritos de las piezas son de lado 1.
Problema 3.
Sea ABCDE un pentágono convexo (las diagonales quedan dentro del pentágono). Sean P, Q, R y S los baricentros de los triángulos ABE, BCE, CDE y DAE, respectivamente.
Demuestra que PQRS es un paralelogramo y que su área es igual a 2/9 del área del cuadrilátero ABCD.
Nota: El baricentro o centroide es el punto donde concurren las medianas.
Segundo Día
Problema 4.
En la figura, escribe un entero positivo dentro de cada triangulito, de manera que el número escrito en cada triangulito que tenga al menos dos vecinos, sea igual a la diferencia de los números escritos en algún par de vecinos de dicho triángulo.
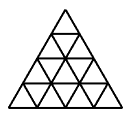
Nota: Dos triangulitos son vecinos si comparten un lado.
Problema 5.
Sea ABC un triángulo acutángulo. C1 y C2 son circunferencias que tienen a los lados AB y CA como diámetros, respectivamente. C 2 corta al lado AB en el punto F (F
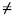 A)
y C1 corta al lado CA en el punto
E (E
A)
y C1 corta al lado CA en el punto
E (E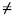 A).
Además, BE corta a C2
en P y CF corta a C1
en Q.
A).
Además, BE corta a C2
en P y CF corta a C1
en Q.
Demuestra que las longitudes de los segmentos AP y AQ son iguales.
Problema 6.
Al escribir un entero n
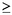 1 como
potencia
de 2 o como suma de potencias de 2, donde cada potencia aparece a
lo más dos veces en la suma, se tiene una
"representación buena" de n.
1 como
potencia
de 2 o como suma de potencias de 2, donde cada potencia aparece a
lo más dos veces en la suma, se tiene una
"representación buena" de n.
- (a) Escribe las 5 representaciones buenas de 10.
- (b) ¿Qué enteros positivos admiten un número par de representaciones buenas?
Nota: Dos representaciones buenas que difieren sólo en el orden de los sumandos se consideran la misma.