Décima Tercera Olimpiada Nacional de
Matemáticas
Oaxaca, Oaxaca, noviembre de 1999
Soluciones
Problema 1
El primer jugador tiene estrategia ganadora. Como 1999 es impar, el
número de fichas con el lado rojo hacia arriba y el número
de fichas con el lado negro hacia arriba son distintos. Entonces, el
primer jugador en su turno puede hacer que el número de fichas
rojas sea igual al número de fichas negras quitando de las que haya
más. No importa qué haga el segundo jugador,
dejará cantidades diferentes de fichas rojas y
negras. Después el primer jugador vuelve a ahcer que haya el mismo
número de fichas rojas que negras. Como al segundo siempre le toca
jugar cuando hay la misma cantidad de rojas que negras, no puede evitar
dejar cantidades diferentes de fichas rojas y negras, por lo tanto gana el
primero.
Problema 2
Supongamos que sí los hay, y sea p el primer primo y
r la diferencia de la progresión. Así, la
progresión es:
p, p+r, p+2r, ... p+1998r.
El primo p no puede ser ninguno de los primero
primos: 2,3,...,1997, ya que si es alguno de estos entonces p+pr,
que está en la progresión, no es primo. Así,
p 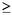 1999. 1999.
Como p es impar y p+r es primo, entonces r es
par. Todos los números pares son de la forma 6n o
6n+2 o 6n-2. Veamos ahora que r no puede ser ni de la
forma 6n+2 ni de la forma 6n-2. En efecto, como p es primo,
éste es de la forma 6k+1 o 6k-1. En cualquiera d elos
cuatro casos hay en la progresión un múltiplo de 3:
p+r = (6k+1)+(6n+2)
p+2r = (6k+1)+(6n-2)
p+2r = (6k-1)+(6n+2)
p+r = (6k-1)+(6n-2)
Por lo tanto, r es de la forma 6n y entonces la
progresión es:
p, p+6n, ..., p+1998(6n).
Pero p 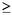 1999 y n 1999 y n 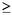 1 implican que p+1998(6n) 1 implican que p+1998(6n) 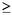 1999+11988=13985 > 12345. 1999+11988=13985 > 12345.
Así los números p+jr no pueden ser todos menores
que 12345.
Problema 3
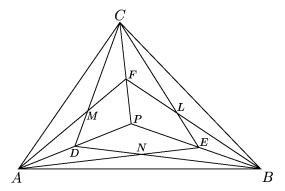
(a) Como en el triángulo ABP, BD y AE son
medianas se tiene que N es el centroide del triángulo
ABP, y como las medianas dividen al triángulo en seis
triángulos de la misma área se tiene que
área (PDNE) = 1/3 área
(ABP)
Análogamente área (PELF) = 1/3
área (BCP) y
área (PFMD) = 1/3 área (CAP)
por lo que concluimos
que:
área (DNELFM) = 1/3 área
(ABC)
(b) Considere el triángulo CDE. Como
CM/MD =
CL/LE se tiene que ML y DE son
paralelas, si Q es el punto de intersección de DL y
EM se tiene que los triángulos QDE y QLM son
semejantes, por lo que: DQ/QL =
EQ/QM =
3/2, o sea DL y EM se cortan en el
punto Q que divide a los segmentos en razón 3:2. Con
el mismo argumento se muestra que FN y DL se cortan en un
punto que los divide en razón 3:2, y por lo tanto es el
mismo punto Q.
Problema 4
Supongamos que no hay puntos marcados a distancia
1/2 de la orilla de la cuadrícula. Probaremos
que hay dos puntos marcados a distancia menor o igual que 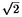 . Como no hay puntos marcados a
distancia
1/2 de la orilla, entonces todos los marcados
están en la cuadrícula central de 6 x 6. Dividimos esta
cuadrícula en 9 cuadrados de 2 x 2. Al haber 10 puntos marcados
forzosamente habrá dos en un mismo cuadrado de 2 x 2. Esos dos
puntos están a distancia menor o igual que . Como no hay puntos marcados a
distancia
1/2 de la orilla, entonces todos los marcados
están en la cuadrícula central de 6 x 6. Dividimos esta
cuadrícula en 9 cuadrados de 2 x 2. Al haber 10 puntos marcados
forzosamente habrá dos en un mismo cuadrado de 2 x 2. Esos dos
puntos están a distancia menor o igual que 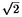
Problema 5
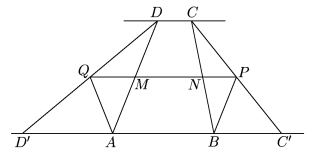
Sean C' y D' los puntos de intersección de
CP con AB y de
DQ
con AB. Como AB es paralela a CD y por ser CP
bisectriz tenemos que
 PCB = PCB =  BC'P, luego BC'P, luego  BCP y BCP y  BC'P son
congruentes,
por
lo que son rectángulos y CP = PC'. Análogamente BC'P son
congruentes,
por
lo que son rectángulos y CP = PC'. Análogamente
 ADQ y ADQ y  AD'Q son
triángulos rectángulos congruentes por lo que DQ =
QD'. AD'Q son
triángulos rectángulos congruentes por lo que DQ =
QD'.
Entonces PQ||AB, además si M y N son los
puntos de
intersección de PQ con AD y BC
respectivamente, se tiene que
M y N
son puntos medios y que MN = 1/2(AB + CD).
Como M es punto medio de la hipotenusa del  ADQ tenemos que QM = AM =
1/2AD, análogamente
NP = BN = 1/2BC, por lo tanto PQ =
1/2(AB + BC + CD + DA). ADQ tenemos que QM = AM =
1/2AD, análogamente
NP = BN = 1/2BC, por lo tanto PQ =
1/2(AB + BC + CD + DA).
Problema 6
Tomamos un polígono ortogonal cualquiera y lo colocamos con sus
lados sobre las líneas de una cuadrícula infinita. Pintamos
la cuadrícula como tablero de ajedrez. Debemos probar que el
polígono tiene al menos un lado par suponiendo que es posible
llenarlo con rectángulos de 2 x 1. Probaremos algo un
poco
más fuerte: que si un polígono ortogonal de n lados tiene
todos los lados impares, entonces no es posible que tenga el mismo
número de cuadros blancos que negros y, de hecho, probraremos que
el número B de cuadros blancos y N de cuadros negros
cumplen |N-B|=1/4n. Asignamos a cada
cuadro
negro del
interior del polígono 4, 1 por cada lado y a cada
cuadro blanco
asignamos -1, -1 por cada lado. La suma de los valores
asignados a los
cuadros es claramente 4(N-B). Por otra parte, la
contribución
total
de cada segmento del interior es 0: 1 por ser lado de un
cuadro negro y -1
por ser lado de un cuadro blanco. Entonces, la suma de los valores
asignados a los cuadros es igual a la suma de los valores asignados a los
segmentos de la orilla del polígono. Pero si todos los lados tienen
longitud impar, la suma de los valores de los segmentos en cada lado es
siuempre 1 o siempre -1. Por lo tanto, 4(N-B) = n o
-n, es decir,
|N-B|=1/4n.
|







