|
|
Séptima Olimpiada Nacional de Matemáticas
Acapulco, Guerrero, noviembre de 1993
Primer Día
Problema 1.
Sea ABC un triángulo rectrángulo en A. Se
construyen exteriormente a este triángulos rectángulos
isósceles AEC y ADB con hipotenusas AC y
AB, respectivamente. Sea O el punto medio de BC y
sean E' y D' los puntos de intersección de OE
y OD con DB y EC, respectivamente. Calcule el
área del cuadrilátero DED'E' en función de los
lados del triángulo ABC.
Problema 2.
Encuentre los números del 100 al 999 tales que la suma de los cubos
de sus dígitos sea igual al número.
Problema 3.
Dentro de un pentágono de área 1993 se
encuentran 995 puntos. Considere esos puntos junto con los vértices
del pentágono. Muestre que de todos los triángulos que se
pueden formar con los 1000 puntos anteriores, hay al menos uno de
área menor o igual a uno.
Segundo Día
Problema 4.
Para cualquier número entero n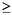 0 se
define: 0 se
define:
(i) f(n,0)=1 y f(n,n)=1
(ii) f(n,k)=f(n-1,k-1)+f(n-1,k) para 0<k<n.
¿Cuántos cálculos se tienen que hacer para encontrar el
valor de f(3991,1993), sin contar aquéllos de la forma
f(n,0) y f(n,n)?
Problema 5.
Por un punto O de una circunferencia se tienen tres cuerdas
que sirven como diámetros de tres circunferencias. Además
del punto común O, las circunferencias se intersectan por
parejas en otros tres puntos. Demuestre que tales puntos son colineales.
Problema 6.
Sean f(x)=x(x+1)(x+2)(x+3)+1 y p un número
impar. Pruebe que existe un entero n tal que p divide a
f(n) si y sólo si existe un entero m tal que p
si divide a m2 - 5.
|







