|
|
Quinta Olimpiada Nacional de Matemáticas
Oaxtepec, Morelos, noviembre de 1991
Primer Día
Problema 1.
Calcule la suma de todas las fracciones positivas
irreducibles
(simplificadas) menores que uno cuyo denominador es 1991.
Problema 2.
Una compañía de n soldados es tal que
(1) n es un número capicúa (es decir, se lee de la
misma
manera al derecho que al revés, por ejemplo 12421 ó 523325),
(2) Si los soldados se forman:
(i) de 3 en 3, quedan 2 soldados en la última fila,
(ii) de 4 en 4, quedan 3 soldados en la última fila,
(iii) de 5 en 5, quedan 5 soldados en la última fila,
(a) ¿Cuál es el mínimo número n tal que
se satisfacen (1) y (2).
(b) Demuestre que hay una infinidad de números n que
satisfacen (1) y (2).
Problema 3.
Se tienen cuatro canicas de radio uno colocadas en el espacio de tal
manera que cada una de ellas es tangente a las otras 3. ¿Cuál
es el radio de la menor esfera que contiene a las canicas?
Segundo Día
Problema 4.
Considere un cuadrilátero convexo ABCD en el que las
diagonales AC y BD se cortan formando ángulo recto.
Sean M,N,R y S los puntos medios de los
segmentos AB, BD, CD y AD, respectivamente.
Sean W, AD, AB y BC, respectivamente. Pruebe
que todos los puntos M,N, R, S, W,
X, Y, y Z están sobre una misma
circunferencia.
Problema 5.
La suma de los cuadrados de dos números consecutivos pueden ser un
cuadrado perfecto, por ejemplo
32+42=52.
(a) Pruebe que la suma de los cuadrados de m enteros consecutivos
no puede
ser un cuadrado para m= 3 y 6.
(b) Encuentre un ejemplo de 11 números positivos consecutivos cuya
suma de cuadrados sea un cuadrado perfecto.
Problema 6.
En un polígono de n lados (n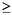 4) se
considera una familia T de triángulos formados con los
vértices del polígono con la propiedad de que cada dos
triángulos de la familia cumplen una de las siguientes dos
condiciones:
(a) No tienen vértices en común,
(b) Tienen 2 vértices en común.
Demuestre que T tiene a lo más n triángulos.
|
